

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
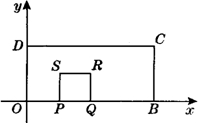 28、如图所示,在直角坐标系中,矩形OBCD的边长OB=4,OD=2.
28、如图所示,在直角坐标系中,矩形OBCD的边长OB=4,OD=2.查看答案和解析>>
科目:初中数学 来源: 题型:
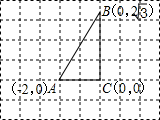 BC的2倍,“宝藏”就在矩形未知的顶点处,那么“宝藏”的位置可能是
BC的2倍,“宝藏”就在矩形未知的顶点处,那么“宝藏”的位置可能是查看答案和解析>>
科目:初中数学 来源: 题型:
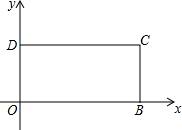 OB方向运动,运动速度是1个单位/秒,运动时间为t秒,直到点P与点B重合为止.
OB方向运动,运动速度是1个单位/秒,运动时间为t秒,直到点P与点B重合为止.查看答案和解析>>
科目:初中数学 来源: 题型:
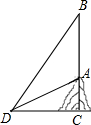 (2013•龙湾区一模)如图,热气球从山顶A竖直上升至点B需25秒,点D在地面上,DC⊥AB,垂足为C,从地面上点D分别仰视A,B两点,测得∠ADC=20°,∠BDC=60°,若CD=130米.求该热气球从山顶A竖直上升至点B的平均速度.(结果精确到0.1米/秒)
(2013•龙湾区一模)如图,热气球从山顶A竖直上升至点B需25秒,点D在地面上,DC⊥AB,垂足为C,从地面上点D分别仰视A,B两点,测得∠ADC=20°,∠BDC=60°,若CD=130米.求该热气球从山顶A竖直上升至点B的平均速度.(结果精确到0.1米/秒)查看答案和解析>>
科目:初中数学 来源:中学学习一本通 数学 九年级下册 北师大课标 题型:044
如图所示,在小山的东侧A处有一热气球沿着与竖直方向夹角为![]() 的方向向东飞行,每分钟飞行28 m,半小时后到达C处,这时气球上的人发现,在A处的正西方向有一处着火点B,5分钟后,在D处测得着火点日的俯角是
的方向向东飞行,每分钟飞行28 m,半小时后到达C处,这时气球上的人发现,在A处的正西方向有一处着火点B,5分钟后,在D处测得着火点日的俯角是![]() ,求热气球升空点A与着火点B的距离.(结果精确到l m)
,求热气球升空点A与着火点B的距离.(结果精确到l m)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com