
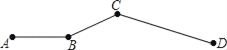
【题目】如图,老王开车从A到D,全程共72千米.其中AB段为平地,车速是30千米/小时,BC段为上山路,车速是22.5千米/小时,CD段为下山路,车速是36千米/小时,已知下山路是上山路的2倍.
(1)若AB=6千米,老王开车从A到D共需多少时间?
(2)当BC的长度在一定范围内变化时,老王开车从A到D所需时间是否会改变?为什么?(给出计算过程)
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】七![]() 班派出
班派出![]() 名同学参加数学竞赛,老师以
名同学参加数学竞赛,老师以![]() 分为基准,把分数超过
分为基准,把分数超过![]() 分的部分记为正数,不足部分记为负数.评分记录如下:
分的部分记为正数,不足部分记为负数.评分记录如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 这
这![]() 名同学中最高分和最低分各是多少?
名同学中最高分和最低分各是多少?
![]() 超过基准分的和低于基准分的各有多少人?
超过基准分的和低于基准分的各有多少人?
![]() 这十二名同学的平均成绩是多少?
这十二名同学的平均成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E,F分别是边AB,CD的中点,(1)求证:△CFB≌△AED;
(2)若∠ADB=90°,判断四边形BFDE的形状,并说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
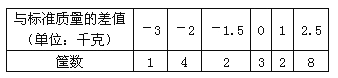
(1)20筐白菜中,最重的一筐比最轻的一筐重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价26元,则出售这20筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求1+2+22+23+…+22016的值,可设S=1+2+22+23+…+22016 , 于是2S=2+22+23+…+22017 , 因此2S﹣S=22017﹣1,所以S=22017﹣1.我们把这种求和方法叫错位相减法.仿照上述的思路方法,计算出1+5+52+53+…+52016的值为( )
A.52017﹣1
B.52016﹣1
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题:
(1)(-78) +(+5)+(+78) (2)(+23)+(-17)+(+6)+(-22)
(3)[45-(![]() -
-![]() +
+![]() )×36]÷5 (4)99
)×36]÷5 (4)99![]() ×(-36)
×(-36)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).

请回答:BC+DE的值为________
参考小明思考问题的方法,解决问题:
如图3,已知ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a﹣2b,2﹣4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为( )
A.(﹣3,7)
B.(﹣1,7)
C.(﹣4,10)
D.(0,10)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时.求证:CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;
①请直接写出CF,BC,CD三条线段之间的关系;
②若正方形ADEF的边长为2![]() ,对角线AE,DF相交于点O,连接OC.求OC的长度.
,对角线AE,DF相交于点O,连接OC.求OC的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com