
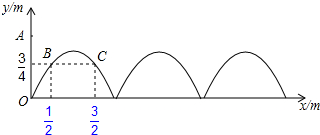
分析 (1)根据题意求得B($\frac{1}{2}$,$\frac{3}{4}$),C($\frac{3}{2}$,$\frac{3}{4}$),解方程组求得拋物线的函数关系式为y=-x2+2x;根据抛物线的顶点坐标公式得到结果;
(2)令y=0,即-x2+2x=0,解方程得到x1=0,x2=2,即可得到结论.
解答 解:(1)根据题意得:B($\frac{1}{2}$,$\frac{3}{4}$),C($\frac{3}{2}$,$\frac{3}{4}$),
把B,C代入y=ax2+bx得$\left\{\begin{array}{l}{\frac{3}{4}=\frac{1}{4}a+\frac{1}{2}b}\\{\frac{3}{4}=\frac{9}{4}a+\frac{3}{2}b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$,
∴拋物线的函数关系式为y=-x2+2x;
∴图案最高点到地面的距离=$\frac{-{2}^{2}}{4×(-1)}$=1;
(2)令y=0,即-x2+2x=0,
∴x1=0,x2=2,
∴10÷2=5,
∴最多可以连续绘制5个这样的拋物线型图案.
点评 本题考查了二次函数的应用,待定系数法求二次函数的解析式,正确的求出二次函数的解析式是解题的关键.


科目:初中数学 来源: 题型:填空题
 如图,在菱形ABCD中,AB=5,AC=8,点P是对角线AC上的一个动点,过点P作EF⊥AC分别交AD、AB于点E、F,将△AEF沿EF折叠,点A落在点A′处,当△A′BC是等腰三角形时,AP的长为$\frac{3}{2}$或$\frac{39}{16}$.
如图,在菱形ABCD中,AB=5,AC=8,点P是对角线AC上的一个动点,过点P作EF⊥AC分别交AD、AB于点E、F,将△AEF沿EF折叠,点A落在点A′处,当△A′BC是等腰三角形时,AP的长为$\frac{3}{2}$或$\frac{39}{16}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 甲方案 | 乙方案 | |
| 门号的月租费(元) | 400 | 600 |
| MAT手机价格(元) | 15000 | 13000 |
| 注意事项:以上方案两年内不可变更月租费 | ||
| A. | 500 | B. | 516 | C. | 517 | D. | 600 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
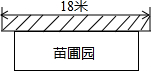 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
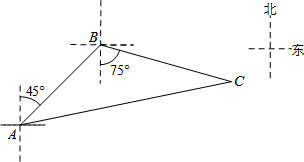 如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com