
【题目】如图,在ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F,试判断四边形AECF是不是平行四边形,并说明理由. 
【答案】解:四边形AECF是平行四边形. 理由如下:
∵AE⊥BD于点E,CF⊥BD于点F,
∴∠AEF=∠CFE=90°,
∴AE∥CF(内错角相等,两直线平行),
在平行四边形ABCD中,AB=CD,AB∥CD,
∴∠ABE=∠CDF,
在△ABE与△DCF中,  ,
,
∴△ABE≌△CDF(AAS),
∴AE=CF,
∴四边形AECF是平行四边形(有一组对边平行且相等的四边形是平行四边形)
【解析】根据垂直,利用内错角相等两直线平行可得AE∥CF,在根据平行四边形的性质证明△ABE与△DCF全等,根据全等三角形对应边相等可得AE=CF,然后根据有一组对边平行且相等的四边形是平行四边形即可证明.
【考点精析】根据题目的已知条件,利用平行四边形的判定与性质的相关知识可以得到问题的答案,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解答后面的问题.
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得 ![]() ,(x、y为正整数)∴
,(x、y为正整数)∴ ![]() 则有0<x<6.又
则有0<x<6.又 ![]() 为正整数,则
为正整数,则 ![]() 为正整数.
为正整数.
由2与3互质,可知:x为3的倍数,从而x=3,代入 ![]() .
.
∴2x+3y=12的正整数解为 ![]()
问题:
(1)请你写出方程2x+y=5的一组正整数解
(2)若 ![]() 为自然数,则满足条件的x值有( )个;
为自然数,则满足条件的x值有( )个;
A.2
B.3
C.4
D.5
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为10,则平行四边形ABCD的周长为 . 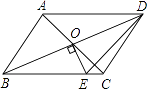
查看答案和解析>>
科目:初中数学 来源: 题型:
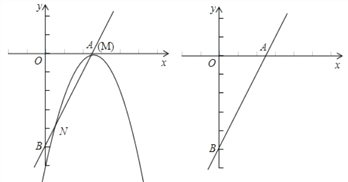
【题目】已知直线y=2x-5与x轴和y轴分别交于点A和点B,抛物线y=-x2+bx+c的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.
(1)如图,当点M与点A重合时,求抛物线的解析式;
(2)在(1)的条件下,求点N的坐标和线段MN的长;
(3)抛物线y=-x2+bx+c在直线AB上平移,是否存在点M,使得△OMN与△AOB相似?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在抄分解因式的题目时,不小心漏抄了二项式x2-□y2(“□”表示漏抄的式子)中y2前的式子,且该二项式能分解因式,那么他漏抄在作业本上的式子不可能是下列中的( )
A. x B. 4 C. -4 D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从⊙O外一点A引⊙O的切线AB,切点为B,连接AO并延长交⊙O于点C,点D.连接BC.
(1)如图1,若∠A=26°,求∠C的度数;
(2)如图2,若AE平分∠BAC,交BC于点E.求∠AEB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l分别交x轴、y轴于A、B两点,OA<OB,且OA、OB的长分别是一元二次方程x2-7x+12=0的两根.

(1)求直线AB的函数表达式;
(2)若在y轴上取一点P,使△ABP是等腰三角形,则请直接写出满足条件的所有点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com