
如图,已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG,
(1)求证:直线EP为⊙O的切线;
(2)点P在劣弧AC上运动,其他条件不变,若BG2=BF•BO.试证明BG=PG;
(3)在满足(2)的条件下,已知⊙O的半径为3,sinB=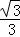 .求弦CD的长.
.求弦CD的长.
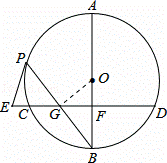

(1)证明:连接OP,∵EP=EG,∴∠EPG=∠EGP,
又∵∠EPG=∠BGF,∴∠EPG=∠BGF,∵OP=OB,
∴∠OPB=∠OBP,∵CD⊥AB,∴∠BFG=∠BGF+∠OBP=90°,∴∠EPG+∠OPB=90°,
∴直线EP为⊙O的切线;
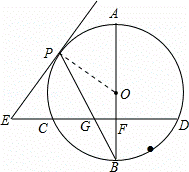
 (2)证明:如图,连接OG,
(2)证明:如图,连接OG,
∵BG2=BF•BO,∴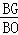 =
=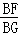 ,∴△BFG∽△BGO,
,∴△BFG∽△BGO,
∴∠BGO=∠BFG=90°,∴BG=PG;
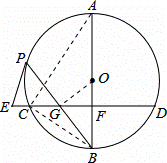
(3)解:如图,连接AC、BC、OG,
∵sinB=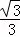 ,∴
,∴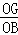 =
=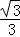 ,∵OB=r=3,∴OG=
,∵OB=r=3,∴OG=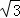 ,
,
由(2)得∠EPG+∠OPB=90°,
∠B+∠BGF=∠OGF+∠BGO=90°,∴∠B=∠OGF,
∴sin∠OGF=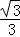 =
=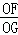 ∴OF=1,
∴OF=1,
∴BF=BO﹣OF=3﹣1=2,FA=OF+OA=1+3=4,
在RT△BCA中,
CF2=BF•FA,∴CF= =
=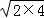 =2
=2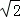 .∴CD=2CF=4
.∴CD=2CF=4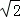 .
.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
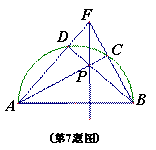
如图,点P在以AB为直径的半圆内,连AP、BP,并延长分别交半圆于点C、D,连接AD、BC并延长交于点F,作直线PF,下列说法正确的是:
①AC垂直平分BF;②AC平分∠BAF;③PF⊥AB;④BD⊥AF.
A.①② B.①④
C.②④ D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
记者小张要了解市民对“雾霾天气产生的主要成因”的看法,随机调查了某区的部分市民,并绘制了如下不完整的统计图表.请根据提供的信息解答下列问题:
(1)填空: ,
,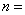 ;
;
(2)请求扇形统计图中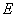 选项所占的百分比为 ;
选项所占的百分比为 ;
(3)若该区人口约有40万人,请估计其中持D选项“观点”的市民人数有多少人?
| 选项 | 观点 |
|
| A | 大气气压低,空气不流动 | 80 |
| B | 地面灰尘大,空气湿度低 |
|
| C | 汽车尾气排放 |
|
| D | 工厂造成的污染 | 120 |
| E | 其他 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:
在学习“二元一次方程组的解”时,数学张老师设计了一个数学活动.有A、B 两组卡片,每组各3张,A组卡片上分别写有0,2,3;B组卡片上分别写有﹣5,﹣1,1.每张卡片除正面写有不同数字外,其余均相同.甲从A组中随机抽取一张记为x,乙从B组中随机抽取一张记为y.
(1)若甲抽出的数字是2,乙抽出的数是﹣1,它们恰好是ax﹣y=5的解,求a的值;
(2)求甲、乙随机抽取一次的数恰好是方程ax﹣y=5的解的概率.(请用树形图或列表法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
在我国南海某海域探明可燃冰储量约有194亿立方米,数字19400000000用科学记数法表示正确的是( )
A.1.94×1010 B. 0.194×1010 C. 19.4×109 D. 1.94×109
查看答案和解析>>
科目:初中数学 来源: 题型:
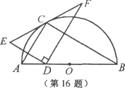
如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为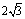 ;③当AD=2时,EF与半圆相切;④若点F恰好落在BC上,则AD=
;③当AD=2时,EF与半圆相切;④若点F恰好落在BC上,则AD=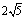 ;⑤当点D从点A运动到点B时,线段EF扫过的面积是
;⑤当点D从点A运动到点B时,线段EF扫过的面积是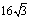 .其中正确结论的序号是 .
.其中正确结论的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com