
【题目】 如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=3∠BCF,∠ACF=20°.
(1)求∠FEC的度数;
(2)若∠BAC=3∠B,求证:AB⊥AC;
(3)当∠DAB=______度时,∠BAC=∠AEC.(请直接填出结果,不用证明)
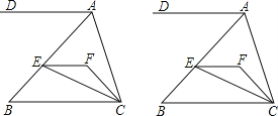
【答案】(1)20°;(2)详见解析;(3)50
【解析】
(1)先根据CE平分∠BCF,设∠BCE=∠ECF=![]() ∠BCF=x.由∠DAC=3∠BCF可得出∠DAC=6x.根据AD∥EF,AD∥BC,得出EF∥BC,由平行线的性质即可得出x的值,进而得出结论;
∠BCF=x.由∠DAC=3∠BCF可得出∠DAC=6x.根据AD∥EF,AD∥BC,得出EF∥BC,由平行线的性质即可得出x的值,进而得出结论;
(2)根据AD∥BC可知∠DAB=∠B,再由∠BAC=3∠B得出∠DAC=4∠B=120°,故∠B=30°,∠BAC=90°,由此可得出结论;
(3)根据(1)可得出∠BCF的度数,设∠BAD=∠B=α,由∠BAC=∠AEC即可得出结论.
解:(1)∵CE平分∠BCF,
∴设∠BCE=∠ECF=![]() ∠BCF=x.
∠BCF=x.
∵∠DAC=3∠BCF,
∴∠DAC=6x.
∵AD∥BC,
∴∠DAC+∠ACB=180°,
∴6x+2x+20°=180°,
∴x=20°,即∠BCE=20°,
∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠BCE=∠FEC=20°;
(2)证明:∵AD∥BC,
∴∠DAB=∠B,
又∵∠BAC=3∠B,
∴∠DAC=4∠B,
由(1)可得∠BCA=20°×3=60°,
∴∠DAC=4∠B=120°,
∴∠B=30°,
∴∠BAC=30°×3=90°,
∴AB⊥AC;
(3)由(1)知∠BCE=20°,
∴∠BCF=40°.
∴∠DAC=3×40°=120°,
∵AD∥BC,
∴可设∠BAD=∠B=α,
∴∠AEC=∠B+∠BCE=α+20°,∠BAC=∠DAC-∠DAB=120°-α,
∴当∠BAC=∠AEC时,α+20°=120°-α,
解得α=50°,
∴∠DAB=50°.
故答案为:50.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,甲、乙两动点分别从正方形 ABCD 的顶点 A、C 同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若甲的速度是乙的速度的 3 倍,则它们第 2018 次相遇在边( )上.
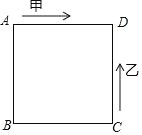
A. CDB. ADC. ABD. BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某乡镇在“精准扶贫”活动中销售一农产品,经分析发现月销售量y(万件)与月份x(月)的关系为:![]() ,每件产品的利润z(元)与月份x(月)的关系如下表:
,每件产品的利润z(元)与月份x(月)的关系如下表:
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
z | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 10 | 10 |
(1)请你根据表格求出每件产品利润z(元)与月份x(月)的关系式;
(2)若月利润w(万元)=当月销售量y(万件)×当月每件产品的利润z(元),求月利润w(万元)与月份x(月)的关系式;
(3)当x为何值时,月利润w有最大值,最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一次函数![]() 的图象上,它们的横坐标依次为
的图象上,它们的横坐标依次为![]() ,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )

A. 1 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
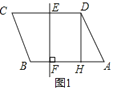
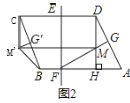
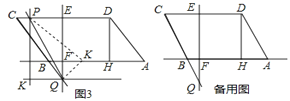
【题目】如图1,在ABCD中,DH⊥AB于点H,CD的垂直平分线交CD于点E,交AB于点F,AB=6,DH=4,BF:FA=1:5.
(1)如图2,作FG⊥AD于点G,交DH于点M,将△DGM沿DC方向平移,得到△CG′M′,连接M′B.
①求四边形BHMM′的面积;
②直线EF上有一动点N,求△DNM周长的最小值.
(2)如图3,延长CB交EF于点Q,过点Q作QK∥AB,过CD边上的动点P作PK∥EF,并与QK交于点K,将△PKQ沿直线PQ翻折,使点K的对应点K′恰好落在直线AB上,求线段CP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知A(-1,4),B(4,2),C(-1,0)三点.
(1)点A关于y轴的对称点A′ 的坐标为 ,点B关于x轴的对称点B′ 的坐标为 ,线段AC的垂直平分线与y轴的交点D的坐标为 ;
(2)求(1)中的△A′ B′ D的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知点D,E,F分别为BC,AD,AE的中点,且S△ABC=4cm2,则阴影部分面积S=( )cm2.
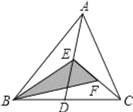
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△EFG≌△NMH, ∠F与∠M是对应角.
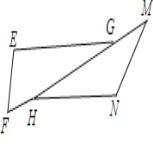
(1)写出相等的线段与相等的角;
(2)若EF=2.1cm,FH=1.1cm,HM=3.3cm,求MN和HG的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com