
分析 (1)根据题意可以列出相应的分式方程,从而可以解答本题,注意分式方程要检验;
(2)根据题意可以得到费用与甲队的函数关系,再根据甲、乙两队施工的总天数不超过26天可以得到相应的不等式,然后根据一次函数的性质即可解答本题.
解答 (1)解:设乙队每天能绿化的面积是xm2,则甲队每天能绿化的面积是2xm2.
$\frac{400}{x}-\frac{400}{2x}=4$,
解得,x=50,
经检验,x=50是原方程的解,
∴2x=100,
答:甲队每天能绿化的面积是100m2,乙队每天能绿化的面积是50m2;
(2)设:甲队施工m天,总费用为W万元.
W=0.6m+$\frac{1800-100m}{50}×0.25$,
化简,得
W=0.1m+9,
∵m+$\frac{1800-100m}{50}$≤26,
解得,m≥10,
∴当m=10时,W取得最小值,此时W=0.1×10+9=10,$\frac{1800-100m}{50}$=16,
答:安排甲队施工10天、乙队的施工16天时,使施工费用最低,最低费用是10万元.
点评 本题考查一次函数的应用、分式方程的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用方程的思想和一次函数的性质解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
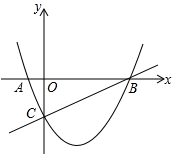 如图,已知抛物线y=ax2-x+c与x轴相交于A、B两点,并与直线y=$\frac{1}{2}$x-2交于B、C两点,其中点C是直线y=x-2与y轴的交点.求抛物线的解析式.
如图,已知抛物线y=ax2-x+c与x轴相交于A、B两点,并与直线y=$\frac{1}{2}$x-2交于B、C两点,其中点C是直线y=x-2与y轴的交点.求抛物线的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 24 | B. | $\sqrt{24}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com