
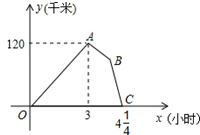
 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下5个结论:
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下5个结论:| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 要解答本题需要熟悉一次函数的图象特征,再根据一次函数的性质和图象结合实际问题对每一项进行分析即可得出答案.
解答 解:①设快递车从甲地到乙地的速度为x千米/时,则
3(x-60)=120,
x=100.
故①正确;
②因为120千米是快递车到达乙地后两车之间的距离,不是甲、乙两地之间的距离,
故②错误;
③快递车由原路返回时,经过$\frac{1}{2}$小时与货车相遇,
故③错误;
④因为快递车到达乙地后缷完物品再另装货物共用45分钟,
所以图中点B的横坐标为3+$\frac{3}{4}$=3$\frac{3}{4}$,
纵坐标为120-60×$\frac{3}{4}$=75,
故④错误;
⑤设快递车从乙地返回时的速度为y千米/时,则返回时与货车共同行驶的时间为(4$\frac{1}{4}$-3$\frac{3}{4}$)小时,此时两车还相距75千米,由题意,得
(y+60)(4$\frac{1}{4}$-3$\frac{3}{4}$)=75,
y=90,
故⑤正确.
其中正确的是:①⑤.
故选:A.
点评 本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题,关键是根据一次函数的性质和图象结合实际问题判断出每一结论是否正确.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:填空题
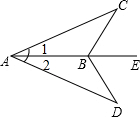 如图,点B在线段AE上,∠1=∠2,如果添加一个条件,即可得到△ABC≌△ABD,那么这个条件可以是AC=AD或∠ABC=∠ABD或∠C=∠D(要求:不在图中添加其他辅助线,写出一个条件即可)
如图,点B在线段AE上,∠1=∠2,如果添加一个条件,即可得到△ABC≌△ABD,那么这个条件可以是AC=AD或∠ABC=∠ABD或∠C=∠D(要求:不在图中添加其他辅助线,写出一个条件即可)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
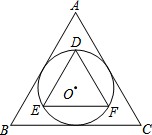 如图,△ABC与△DEF均为等边三角形,⊙O是△ABC的内切圆,同时也是△DEF的外接圆.若AB=1cm,则DE=$\frac{1}{2}$cm.
如图,△ABC与△DEF均为等边三角形,⊙O是△ABC的内切圆,同时也是△DEF的外接圆.若AB=1cm,则DE=$\frac{1}{2}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
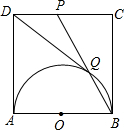 如图,正方形ABCD的边长为1,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结DQ,给出如下结论:①DQ=1;②$\frac{PQ}{BQ}$=$\frac{3}{2}$;③S△PDQ=$\frac{1}{8}$;④cos∠ADQ=$\frac{3}{5}$,其中正确结论是①②④(填写序号)
如图,正方形ABCD的边长为1,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结DQ,给出如下结论:①DQ=1;②$\frac{PQ}{BQ}$=$\frac{3}{2}$;③S△PDQ=$\frac{1}{8}$;④cos∠ADQ=$\frac{3}{5}$,其中正确结论是①②④(填写序号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点A、B的坐标分别为(0,2),(3,4),点P为x轴上的一点,若点B关于直线AP的对称点B′恰好落在x轴上,则点P的坐标为($\frac{4}{3},0$).
如图,点A、B的坐标分别为(0,2),(3,4),点P为x轴上的一点,若点B关于直线AP的对称点B′恰好落在x轴上,则点P的坐标为($\frac{4}{3},0$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A、B两点,其中点A的坐标为(-3,0).
如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A、B两点,其中点A的坐标为(-3,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com