
【题目】如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
解答下列问题:
(1)如果AB=AC,∠BAC=90.
①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为 ,数量关系为 .
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
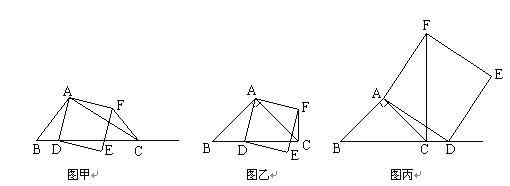
(2)如果AB≠AC,∠BAC≠90,点D在线段BC上运动.
试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?画出相应图形,并说明理由.(画图不写作法)
(3)若AC=![]() ,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
【答案】(1)①CF与BD位置关系是垂 直、数量关系是相 等;
②当点D在BC的延长线上时①的结论仍成立.
由正方形ADEF得 AD="AF" ,∠DAF=90.
∵∠BAC=90,∴∠DAF="∠BAC" , ∴∠DAB=∠FAC,
又AB="AC" ,∴△DAB≌△FAC , ∴CF=BD
∠ACF=∠ABD.
∵∠BAC=90, AB="AC" ,∴∠ABC=45,∴∠ACF=45,
∴∠BCF="∠ACB+∠ACF=" 90.即 CF⊥BD
(2)画图正确
当∠BCA=45时,CF⊥BD(如图丁).
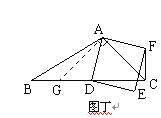
理由是:过点A作AG⊥AC交BC于点G,∴AC=AG
可证:△GAD≌△CAF ∴∠ACF=∠AGD=45
∠BCF="∠ACB+∠ACF=" 90. 即CF⊥BD
(3)当具备∠BCA=45时,
过点A作AQ⊥BC交BC的延长线于点Q,(如图戊)
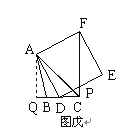
∵DE与CF交于点P时, ∴此时点D位于线段CQ上,
∵∠BCA=45,可求出AQ= CQ=4.设CD="x" ,∴ DQ=4—x,
容易说明△AQD∽△DCP,∴![]() , ∴
, ∴![]() ,
,
![]() .
.
∵0<x≤3 ∴当x=2时,CP有最大值1.
【解析】
(1)首先选择图2证明,由AB=AC,∠BAC=90°,可得:△ABC是等腰直角三角形,又由四边形ADEF是正方形,易证得△ABD≌△ACF(SAS),即可求得:CF=BD,∠ACF=∠B=45°,证得CF⊥BD;
(2)过点A作AG⊥AC交BC于点G,可证△GAD≌△CAF,则∠ACF=∠AGD=45,从而得∠BCF="∠ACB+∠ACF=" 90, 即CF⊥BD。
(3)首先作辅助线:过点A作AG⊥BC,垂足为G,连接CF,易得:△AGD∽△DCP,由相似三角形的对应边成比例,即可求得:AGCP=GDDC,在等腰Rt△AGC中求得AC的值,设GD=x,即可求得CP关于x的二次函数,求得最大值.


科目:初中数学 来源: 题型:
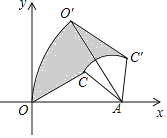
【题目】如图,△OAC的顶点O在坐标原点,OA边在x轴上,OA=2,AC=1,把△OAC绕点A按顺时针方向旋转到△O′AC′,使得点O′的坐标是(1,![]() ),则在旋转过程中线段OC扫过部分(阴影部分)的面积为______.
),则在旋转过程中线段OC扫过部分(阴影部分)的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系中,点![]() 在
在![]() 轴上,点
轴上,点![]() 、
、![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() ,
,![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,
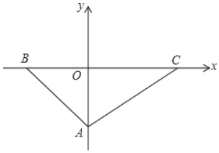
(1)求![]() 三个顶点
三个顶点![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
(2)连接![]() 、
、![]() ,并用含字母
,并用含字母![]() 的式子表示
的式子表示![]() 的面积(
的面积(![]() );
);
(3)在(2)问的条件下,是否存在点![]() ,使
,使![]() 的面积等于
的面积等于![]() 的面积?如果存在,请求出点
的面积?如果存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,
,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() 、
、![]() .
.
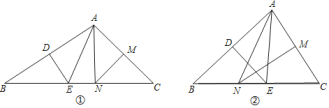
(1)请判断△ANE的周长与AB+AC的和的大小,并说明理由.
(2)①如图①,若∠B=34°,∠C=28°,求![]() 的度数为______;
的度数为______;
②如图②,若![]() ,则
,则![]() 的度数为________;
的度数为________;
③若![]()
![]() ,则
,则![]() 的度数为________.
的度数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)或不等式(组)解应用题:
(1)甲工人接到240个零件的任务,工作1小时后,因要提前完成任务,调来乙和甲合作,合做了5小时完成.已知甲每小时比乙少做4个,那么甲、乙每小时各做多少个?
(2)某工厂准备购进![]() 、
、![]() 两种机器共20台用于生产零件,经调查2台
两种机器共20台用于生产零件,经调查2台![]() 型机器和1台
型机器和1台![]() 型机器价格为18万元,1台
型机器价格为18万元,1台![]() 型机器和2台
型机器和2台![]() 型机器价格为21万元.
型机器价格为21万元.
①求一台![]() 型机器和一台
型机器和一台![]() 型机器价格分别是多少万元?
型机器价格分别是多少万元?
②已知1台![]() 型机器每月可加工零件400个,1台
型机器每月可加工零件400个,1台![]() 型机器每月可加工零件800个,经预算购买两种机器的价格不超过140万元,每月两种机器加工零件总数不低于12400个,那么有哪几种购买方案,哪种方案最省钱?
型机器每月可加工零件800个,经预算购买两种机器的价格不超过140万元,每月两种机器加工零件总数不低于12400个,那么有哪几种购买方案,哪种方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC且AB=BC,DE⊥CD且DE=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )

A. 36B. 48C. 72D. 108
查看答案和解析>>
科目:初中数学 来源: 题型:
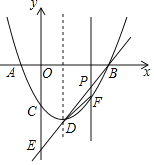
【题目】如图,对称轴为直线x=1的抛物线y=x2﹣bx+c与x轴交于A(x1,0)、B(x2,0)(x1<x2)两点,与y轴交于C点,且![]() +
+![]() =﹣
=﹣![]() .
.
(1)求抛物线的解析式;
(2)抛物线顶点为D,直线BD交y轴于E点;
①设点P为线段BD上一点(点P不与B、D两点重合),过点P作x轴的垂线与抛物线交于点F,求△BDF面积的最大值;
②在线段BD上是否存在点Q,使得∠BDC=∠QCE?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com