
【题目】如图,在等腰直角三角形ABC中,∠C=90°,AB=8![]() ,点O是AB的中点.将一个边长足够大的Rt△DEF的直角顶点E放在点O处,并将其绕点O旋转,始终保持DE与AC边交于点G,EF与BC边交于点H.
,点O是AB的中点.将一个边长足够大的Rt△DEF的直角顶点E放在点O处,并将其绕点O旋转,始终保持DE与AC边交于点G,EF与BC边交于点H.
(1)当点G在AC边什么位置时,四边形CGOH是正方形.
(2)等腰直角三角ABC的边被Rt△DEF覆盖部分的两条线段CG与CH的长度之和是否会发生变化,如不发生变化,请求出CG与CH之和的值:如发生变化,请说明理由.
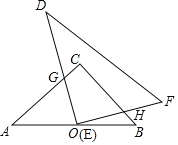
【答案】(1)点G在AC的中点时,四边形CGOH是正方形;(2)CG与CH的和不会发生变化,CG+CH=8.
【解析】
(1)由三角形中位线定理可得OG∥BC,OG=![]() BC,可证四边形CGOH是矩形,由等腰直角三角形的性质可得∠ACO=∠COG=45°,可得CG=GO,可得结论;
BC,可证四边形CGOH是矩形,由等腰直角三角形的性质可得∠ACO=∠COG=45°,可得CG=GO,可得结论;
(2)由“ASA”可证△GOC≌△HOB,可得CG=BH,即可得CG+CH=HB+CH=BC=8.
解:(1)当点G在AC的中点时,四边形CGOH是正方形,
连接CO,
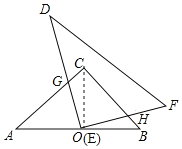
∵O为AB的中点,点G是AC中点,
∴OG∥BC,OG=![]() BC,
BC,
∴∠CGO=∠C=90°,
∵∠GOF=90°,
∴四边形CGOH是矩形,
∵AC=BC,∠ACB=90°,AO=BO,
∴∠ACO=45°,且∠CGO=90°,
∴∠ACO=∠COG=45°,
∴CG=GO,
∴矩形CGOH是正方形;
(2)CG与CH的和不会发生变化,
理由如下:
连接OC,
∵△ABC是等腰直角三角形且点O为中点
∴∠GCO=∠B=45°,∠COB=90°,CO=BO
∵∠DOF=90°=∠COB,
∴∠GOC=∠HOB,且CO=BO,∠GCO=∠B=45°,
∴△GOC≌△HOB(ASA)
∴HB=GC,
∴CG+CH=HB+CH=BC
∵AB=8![]() ,
,
∴BC=AC=8
∴CG+CH=8.


科目:初中数学 来源: 题型:
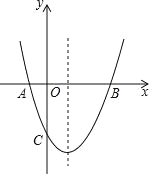
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交于A,B两点(A在B的左侧),顶点为C.
(1)求A,B两点的坐标;
(2)若将该抛物线向上平移t个单位后,它与x轴恰好只有一个交点,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点。
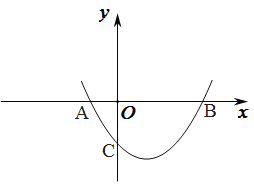
(1)求b、c的值;
(2)P为抛物线上的点,且满足S△PAB=8,求P点的坐标
(3)设抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
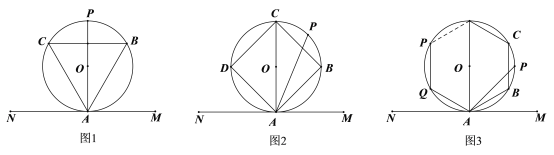
【题目】如图1,![]() 是⊙O内接等边三角形,直线MN与⊙O相切于A点,P是弧BC的中点,则
是⊙O内接等边三角形,直线MN与⊙O相切于A点,P是弧BC的中点,则![]() .
.
(1)如图2,正方形ABCD是⊙O内接正方形,直线MN与⊙O相切于A点,P是弧BC的中点,则![]() ________;
________;
(2)如图3,若正n边形ABC……PQ是⊙O内接正n边形,直线MN与⊙O相切于A点,P是弧BC的中点,若![]() 的度数小于
的度数小于![]() ,则n的最小值是_______.
,则n的最小值是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
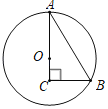
【题目】如图,△ABC中,∠C=90°,∠B=60°,在AC边上取点O画圆,使⊙O经过A、B两点,下列结论中:①AO=BC;②AO=2CO;③延长BC交⊙O与D,则A、B、D是⊙O的三等分点;④以O为圆心,以OC为半径的圆与AB相切.正确的序号是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
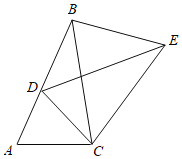
【题目】如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE.
(Ⅰ)求证:∠A=∠EBC;
(Ⅱ)若已知旋转角为50°,∠ACE=130°,求∠CED和∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形木框ABCD中,AB=2AD=4,将其按顺时针变形为ABC′D′,当∠AD′B=90°时,四边形对称中心O经过的路径长为( )
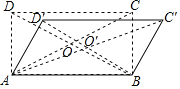
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线C1:y=﹣x2+2x.
(1)补全表格:
抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
y=﹣x2+2x | (1,1) |
|
| (0,0) |
(2)将抛物线C1向上平移3个单位得到抛物线C2,请画出抛物线C1,C2,并直接回答:抛物线C2与x轴的两交点之间的距离是抛物线C1与x轴的两交点之间距离的多少倍.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x+2与x轴交于A、B两点,交y轴于点C.
x+2与x轴交于A、B两点,交y轴于点C.
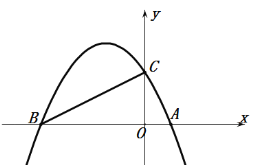
(1)判断△ABC的形状,并说明理由.
(2)在抛物线对称轴上是否存在一点P,使得以A、C、P为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com