
【题目】已知圆E:(x+ ![]() )2+y2=16,点F(
)2+y2=16,点F( ![]() ,0),P是圆E上任意一点,线段PF的垂直平分线和半径PE相交于Q.(Ⅰ)求动点Q的轨迹E的方程; (Ⅱ)直线l过点(1,1),且与轨迹Γ交于A,B两点,点M满足
,0),P是圆E上任意一点,线段PF的垂直平分线和半径PE相交于Q.(Ⅰ)求动点Q的轨迹E的方程; (Ⅱ)直线l过点(1,1),且与轨迹Γ交于A,B两点,点M满足 ![]() =
= ![]() ,点O为坐标原点,延长线段OM与轨迹Γ交于点R,四边形OARB能否为平行四边形?若能,求出此时直线l的方程,若不能,说明理由.
,点O为坐标原点,延长线段OM与轨迹Γ交于点R,四边形OARB能否为平行四边形?若能,求出此时直线l的方程,若不能,说明理由.
【答案】解:(I)∵|QE|+|QF|=|EQ|+|QP|=4,且|EF|=2 ![]() <4, ∴点Q的轨迹是以E,F为焦点的椭圆,
<4, ∴点Q的轨迹是以E,F为焦点的椭圆,
设椭圆方程为 ![]() =1,则2a=4,c=
=1,则2a=4,c= ![]() ,∴a=2,b=
,∴a=2,b= ![]() =1.
=1.
所以点E的轨迹方程为: ![]() +y2=1.
+y2=1.
(II)(1)当直线l与x轴垂直时,直线l的方程为x=1,显然四边形OARB是平行四边形;(2)当直线l与x轴不垂直时,设直线l:y=kx+m,显然k≠0,m≠0,
设A(x1 , y1),B(x2 , y2),M(xM , yM).
联立方程组 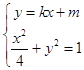 ,得(4k2+1)x2+8kmx+4m2﹣4=0,
,得(4k2+1)x2+8kmx+4m2﹣4=0,
∴x1+x2=﹣ ![]() ,
,
∵ ![]() =
= ![]() ,即M是AB的中点,
,即M是AB的中点,
∴xM= ![]() =﹣
=﹣ ![]() ,yM=kxM+m=
,yM=kxM+m= ![]() ,
,
若四边形OARB是平行四边形,当且仅当AB,OR互相平分,
∴R(﹣ ![]() ,
, ![]() ),
),
代入椭圆方程得: ![]() +
+ ![]() =1,即16k2m2+4m2=16k4+8k2+1,
=1,即16k2m2+4m2=16k4+8k2+1,
又直线l:y=kx+m经过点(1,1),∴m=1﹣k,
∴16k2(1﹣k)2+4(1﹣k)2=16k4+8k2+1,
∴32k3﹣12k2+8k﹣3=0,即(4k2+1)(8k﹣3)=0.
∴k= ![]() ,m=
,m= ![]() ,
,
∴直线l的方程为y= ![]() x+
x+ ![]() 时,四边形OARB是平行四边形,
时,四边形OARB是平行四边形,
综上,直线l的方程为x=1或y= ![]() x+
x+ ![]() .
.
【解析】(I)利用椭圆的定义即可得出E的轨迹方程;(II)讨论直线l的斜率,联立方程组,利用根与系数的关系得出M点坐标,根据平行四边形对角线互相平分得出R点坐标,代入椭圆方程化简即可得出直线l的斜率k.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】已知集合A={x|x2﹣2x<0},B={x|y=log2(x﹣1)},则A∪B=( )
A.(0,+∞)
B.(1,2)
C.(2,+∞)
D.(﹣∞,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=ln2(x﹣1)﹣ ![]() ﹣x+3. (Ⅰ)求函数f(x)的单调区间;
﹣x+3. (Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若当x≥1时,不等式(x+1)x+m≤exx+m恒成立,求实数m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)证明:k∈R,直线y=g(x)都不是曲线y=f(x)的切线;
(2)若x∈[e,e2],使得f(x)≤g(x)+ ![]() 成立,求实数k的取值范围.
成立,求实数k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数列{an}与{bn}满足an=2bn+3(n∈N*),若{bn}的前n项和为Sn= ![]() (3n﹣1)且λan>bn+36(n﹣3)+3λ对一切n∈N*恒成立,则实数λ的取值范围是 .
(3n﹣1)且λan>bn+36(n﹣3)+3λ对一切n∈N*恒成立,则实数λ的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设函数f(x)= ![]() ,则满足f(f(m))=3f(m)的实数m的取值范围是( )
,则满足f(f(m))=3f(m)的实数m的取值范围是( )
A.(﹣∞,0)∪{﹣ ![]() }
}
B.[0,1]
C.[0,+∞)∪{﹣ ![]() }
}
D.[1,+∞)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 25 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |

(1)求出表中M、p及图中a的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间[20,25)内的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣3,﹣1, ![]() ,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组
,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组 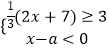 无解,且使关于x的分式方程
无解,且使关于x的分式方程 ![]() ﹣
﹣ ![]() =﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )
=﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )
A.﹣3
B.﹣2
C.﹣ ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路的同侧依次排列着A,C,B三个村庄,某天甲、乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止,从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.求: 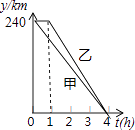
(1)甲的速度是 , 乙的速度是;
(2)分别求出甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系式,并写出取值范围;
(3)若甲、乙两车到C地后继续沿该公路原速度行驶,求甲车出发多少小时,两车相距350km.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com