
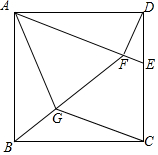
 如图,已知正方形ABCD的边长为3,在CD边上取一点E,使DE=1,连接AE,过点D作DF⊥AE于点F,连接BF过点A作AG⊥BF于点G,连接CG,则CG=$\frac{3}{130}$$\sqrt{6890}$.
如图,已知正方形ABCD的边长为3,在CD边上取一点E,使DE=1,连接AE,过点D作DF⊥AE于点F,连接BF过点A作AG⊥BF于点G,连接CG,则CG=$\frac{3}{130}$$\sqrt{6890}$. 分析 作FM⊥AB于M,MF交CD的延长线于N,作GH⊥AB于H,GK⊥BC于K.则四边形AMND,四边形GHBK是矩形.在Rt△CKG中,利用勾股定理,想办法求出GK、CK即可解决问题.
解答 解:作FM⊥AB于M,MF交CD的延长线于N,作GH⊥AB于H,GK⊥BC于K.则四边形AMND,四边形GHBK是矩形.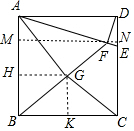
∵四边形ABCD是正方形,
∴AB=CD=BC=AB=3,∠ADC=∠ABC=90°,
在Rt△ADE中,AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{10}$,
∵DF⊥AE,
∴DF=$\frac{AD•DE}{AE}$=$\frac{3\sqrt{10}}{10}$,EF=$\sqrt{D{E}^{2}-D{F}^{2}}$=$\frac{\sqrt{10}}{10}$,
∴FN=$\frac{DF•EF}{DE}$=$\frac{3}{10}$,FM=3-$\frac{3}{10}$=$\frac{27}{10}$,DN=$\frac{9}{10}$
∴BM=AB-AM=3-$\frac{9}{10}$=$\frac{21}{10}$,
在Rt△BMF中,BF=$\sqrt{B{M}^{2}+M{F}^{2}}$=$\frac{3}{10}$$\sqrt{130}$,
∵$\frac{1}{2}$•AB•FM=$\frac{1}{2}$•FB•AG,
∴AG=$\frac{27}{130}$$\sqrt{130}$,
在Rt△ABG中,BG=$\sqrt{A{B}^{2}-A{G}^{2}}$=$\frac{21}{130}$$\sqrt{130}$,
同法HG=$\frac{AG•BG}{AB}$=$\frac{189}{130}$,
在Rt△BHG中,BH=GK=$\sqrt{B{G}^{2}-G{H}^{2}}$=$\frac{147}{130}$,
在Rt△CKG中,CG=$\sqrt{C{K}^{2}+G{K}^{2}}$=$\sqrt{(\frac{147}{130})^{2}+(\frac{201}{130})^{2}}$=$\frac{3}{130}$$\sqrt{6890}$.
故答案为$\frac{3}{130}$$\sqrt{6890}$.
点评 本题考查正方形的性质、勾股定理、面积法等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,计算量比较大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 蔗糖质量 | 4.5 | 5.8 | 5.4 | 6.9 | 4.2 | 7 | 4.9 | 5.8 | 9.8 | 6.8 |
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 蔗糖质量 | 7.4 | 4.9 | 7.8 | 4.1 | 7.2 | 5.8 | 7.6 | 6.8 | 4.5 | 4.9 |
| 酸奶口感最佳的杯数(杯) | 每杯酸奶中添加的蔗糖克数平均值(克) | 每杯酸奶中添加的蔗糖克数的方差 | |
| 学农1班 | x | 6.11 | 2.39 |
| 学农2班 | 6 | 6.1 | 1.81 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{4}$ | B. | $\sqrt{10}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\frac{1}{\sqrt{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 单项式-ab2的次数是2次 | B. | (-2)3中底数是2 | ||
| C. | $\frac{3a{b}^{3}}{5}$的系数是3 | D. | x+3是多项式 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com