
【题目】某社区的6名志愿者,在“十一”假期组织区内的未成年学生到公园秋游,公园的门票为每人40元,现有两种优惠方案,甲方案:志愿者免费,未成年学生按8折收费;乙方案:志愿者和未成年学生都按7折收费,若有![]() 名未成年学生.
名未成年学生.
(1)当![]() 时,甲方案需 元;乙方案需 元;
时,甲方案需 元;乙方案需 元;
(2)用含![]() 的式子表示两种方案各需多少元?
的式子表示两种方案各需多少元?
(3)当![]() 为何值时,甲、乙两种方案是一样的.
为何值时,甲、乙两种方案是一样的.
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() (m为常数)的图像在第一、三象限.
(m为常数)的图像在第一、三象限.
(1)求m的取值范围.
(2)如图,若该反比例函数的图像经过ABOD的顶点D,点A,B的坐标分别为(0,3),(-2,0).
①求出该反比例函数的表达式;
②设P是该反比例函数图像上的一点,若OD=OP,则点P的坐标为________________;若以D,O,P为顶点的三角形是等腰三角形,则满足条件的点P有________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
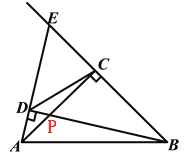
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=![]() ,点P是AC边上的一动点(点P不与端点A、C重合),过点A作AE⊥BP于D,交BC的延长线于点E.
,点P是AC边上的一动点(点P不与端点A、C重合),过点A作AE⊥BP于D,交BC的延长线于点E.
(1)求证:△ACE≌△BCP;
(2)在点P的移动过程中,若AD=DC,试求CP的长;
(3)试探索:在点P的移动过程中,∠ADC的大小是否保持不变?若保持不变,请求出∠ADC的大小;若有变化,请说明变化情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=3x与双曲线y=![]() (k≠0,且x>0)交于点A,点A的横坐标是1.
(k≠0,且x>0)交于点A,点A的横坐标是1.
(1)求点A的坐标及双曲线的解析式;
(2)点B是双曲线上一点,且点B的纵坐标是1,连接OB,AB,求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
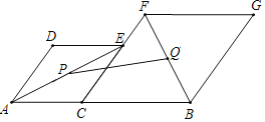
【题目】如图,已知AB=2![]() ,C为线段AB上的一个动点,分别以AC,CB为边在AB的同侧作菱形ACED和菱形CBGF,点C,E,F在一条直线上,∠D=120°.P、Q分别是对角线AE,BF的中点,当点C在线段AB上移动时,点P,Q之间的距离最短为_____(结果保留根号).
,C为线段AB上的一个动点,分别以AC,CB为边在AB的同侧作菱形ACED和菱形CBGF,点C,E,F在一条直线上,∠D=120°.P、Q分别是对角线AE,BF的中点,当点C在线段AB上移动时,点P,Q之间的距离最短为_____(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料,并解答相应的问题:幻方将若干个数组成一个正方形数阵,若任意一行,一列及对角线上的数字之和都相等,则称具有这种性质的数字方阵为“幻方”.中国古代称“幻方”为“河图”、“洛书”等.例如,下面是三个三阶幻方,是将数字1,2,3,4,5,6,7,8,9填入到3×3的方格中得到的,其每行、每列、每条对角线上的三个数之和相等.
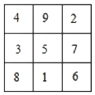
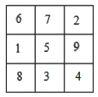
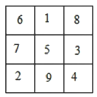
(1)请将下面图1的三阶幻方补充完整;
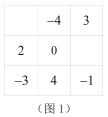

(2)设图2的三阶幻方中间的数字是![]() (其中
(其中![]() 为正整数),请用含
为正整数),请用含![]() 的代数式将图2的幻方填充完整.
的代数式将图2的幻方填充完整.
(3)若设(2)题幻方中9个数的和为![]() ,则
,则![]() 与中间的数字
与中间的数字![]() 之间的数量关系为 .
之间的数量关系为 .
(4)现要用9个数-5,-4,-3,-2,-1,0,1,2,3构造一个三阶幻方.请将构造的幻方填写在下面![]() 的方格中.
的方格中.
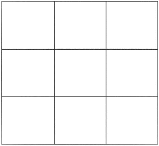
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点M的坐标为(x1,y1),点的坐标为(x2,y2),且x1≠x2,y1≠y2,以MN为边构造菱形,若该菱形的两条对角分平行于x轴、y轴,则称该菱形为边的“坐标菱形”.

(1)已知点A(2,0),B(0,3),则以AB为边的“坐标菱形”的面积为 ;
(2)若点C(1,2),点D在直线x=5上,以CD为边的“坐标菱形”为正方形,求直线CD的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C、D是半圆O上的三等分点,直径AB=4,连接AD、AC,DE⊥AB,垂足为E,DE交AC于点F.
(1)求∠AFE的度数;
(3)求阴影部分的面积(结果保留π和根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.
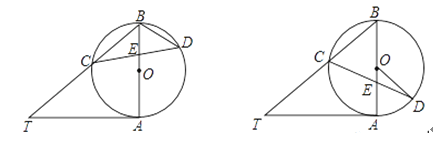
(1)如图①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC,求∠CDO的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com