

分析 (1)首先作OD⊥AC,判断出OD∥BC,推得△AOD∽△ABC,即可判断出$\frac{OD}{BC}$=$\frac{AO}{AB}$;然后根据AO:OB=2:5,求出OD的长度,即可求出点O到AC的距离是多少.
(2)①首先根据△AOP∽△PCQ,可得∠AOP=∠PCQ=90°,∠OAP=∠CPQ,所以PQ∥AB,据此推得$\frac{CP}{AC}=\frac{PQ}{AB}$;然后设AP=x,则CP=4-x,$\frac{4-x}{4}$=$\frac{PQ}{5}$,据此求出PQ的值,进而求出x的值是多少即可.
②首先作OD⊥AC,判断出OD∥BC,推得△AOD∽△ABC,求出AD、PD的长度各是多少;然后根据相似三角形判定的方法,判断出△POD∽QPC,即可推得$\frac{OD}{PC}$=$\frac{PD}{QC}$,据此求出y关于x的函数解析式.并写出函数定义域即可.
③根据题意,分两种情况:当OQ∥AC时;当PQ平分∠CQO时;然后根据相似三角形的性质,分类讨论,求出AP长是多少即可.
解答 解:(1)如图1,作OD⊥AC,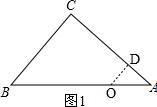 ,
,
∵∠ACB=90°,
∴BC⊥AC,
∵OD⊥AC,BC⊥AC,
∴OD∥BC,
∴△AOD∽△ABC,
∴$\frac{OD}{BC}$=$\frac{AO}{AB}$,
又∵AO:OB=2:5,
∴$\frac{OD}{3}$=$\frac{2}{2+5}$=$\frac{2}{7}$,
解得OD=$\frac{6}{7}$,
即点O到AC的距离是$\frac{6}{7}$.
(2)①如图2, ,
,
∵∠ACB=90°,AC=4,BC=3,
∴AB=$\sqrt{{AC}^{2}{+BC}^{2}}$=$\sqrt{{4}^{2}{+3}^{2}}$=5,
∵AO:OB=2:5,
∴AO=5×$\frac{2}{2+5}$=$\frac{10}{7}$;
∵△AOP∽△PCQ,
∴∠AOP=∠PCQ=90°,∠OAP=∠CPQ,
∴PQ∥AB,
∴$\frac{CP}{AC}=\frac{PQ}{AB}$,
设AP=x,则CP=4-x,
∴$\frac{4-x}{4}$=$\frac{PQ}{5}$,
解得PQ=5-1.25x,
∵∠OAP=∠CPQ,
∴cos∠OAP=cos∠CPQ,
∴$\frac{AO}{AP}=\frac{CP}{PQ}$,
∴$\frac{\frac{10}{7}}{x}=\frac{4-x}{5-1.25x}$,
解得x=$\frac{25}{14}$,
∴若△AOP∽△PCQ,AP的长是$\frac{25}{14}$.
②如图3,作OD⊥AC,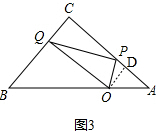 ,
,
∵OD⊥AC,BC⊥AC,
∴OD∥BC,
∴△AOD∽△ABC,
∴$\frac{AD}{AC}$=$\frac{AO}{AB}$,
又∵AO:OB=2:5,
∴$\frac{AD}{4}$=$\frac{2}{2+5}$=$\frac{2}{7}$,
解得AD=$\frac{8}{7}$,PD=x-$\frac{8}{7}$,
∵PQ⊥OP,
∴∠OPD+∠CPQ=90°,
又∵∠PQC+∠CPQ=90°,
∴∠OPD=∠PQC,
在△POD和QPC中,
$\left\{\begin{array}{l}{∠OPD=∠PQC}\\{∠PDO=∠QCP=90°}\end{array}\right.$
∴△POD∽QPC,
∴$\frac{OD}{PC}$=$\frac{PD}{QC}$,
∴$\frac{\frac{6}{7}}{4-x}=\frac{x-\frac{8}{7}}{y}$,
∴y=-$\frac{7}{6}$x2+6x-$\frac{16}{3}$($\frac{8}{7}$<x<4).
③如图4,当OQ∥AC时,△OPQ∽△CPQ,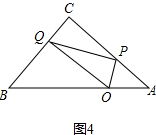 ,
,
∵OQ∥AC,
∴$\frac{CQ}{BC}=\frac{AO}{AB}$,
∴$\frac{CQ}{3}=\frac{2}{2+5}=\frac{2}{7}$,
解得CQ=$\frac{6}{7}$,
∴$\frac{6}{7}$=-$\frac{7}{6}$AP2+6AP-$\frac{16}{3}$,
解得AP=$\frac{26}{7}$或$\frac{10}{7}$.
如图5,作PE⊥OQ于点E,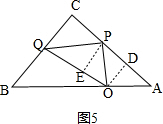 ,
,
当PQ平分∠CQO时,△OPQ∽△CPQ,
∵∠CQP=∠PQE,PC⊥BC,PE⊥OQ,
∴PC=PE,
∵∠POQ=∠CPQ,∠DOP=∠CPQ,
∴∠POQ=∠DOP,
又∵PD⊥OD,PE⊥OE,
∴PD=PE,
∴PC=PD,
即点P为CD的中点,
由AP-AD=AC-AP,
可得AP-$\frac{8}{7}$=4-AP,
解得AP=$\frac{18}{7}$,
综上,可得
当△OPQ∽△CPQ时,AP=$\frac{26}{7}$、$\frac{10}{7}$或$\frac{18}{7}$.
点评 (1)此题主要考查了三角形相似的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.
(2)此题还考查了考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,要熟练掌握.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
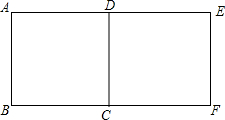 如图所示,图中的两个正方形可以通过平移的方法互相得到,如果将其中一个正方形绕某个点旋转一个角度后能与另一个重合,问:这样的点共有几个?请在图中分别标出它们.
如图所示,图中的两个正方形可以通过平移的方法互相得到,如果将其中一个正方形绕某个点旋转一个角度后能与另一个重合,问:这样的点共有几个?请在图中分别标出它们.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com