
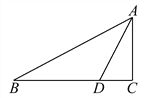
【题目】如图,已知在Rt△ABC中,∠C=90°,D是BC边上一点,AC=6,CD=3,∠ADC=α.
(1)试写出α的正弦、余弦、正切这三个函数值;
(2)若∠B与∠ADC互余,求BD及AB的长.
【答案】(1)sinα=![]() ,cosα=
,cosα=![]() ,tanα=2;(2)BD=9,AB=6
,tanα=2;(2)BD=9,AB=6![]() .
.
【解析】试题分析:(1)利用勾股定理求出AD的长度,再根据公式分别求出sinα、cosα、tanα的值;(2)由已知条件不难推出∠DAC=∠B,即tan∠DAC=tan∠B,算出tan∠DAC,即可算出BC、AD的长度,从而算出BD 的长度.
试题解析:
∵AC=6,CD=3,∴AD=![]() =3
=3![]() ,
,
∴sinα=![]() =
=![]() =
=![]() ,cosα=
,cosα=![]() =
=![]() =
=![]() ,tanα=
,tanα=![]() =
=![]() =2;
=2;
(2)∵∠C=90°,∴∠ADC+∠DAC=90°,
∵∠B+∠ADC=90°,∴∠DAC=∠B,
∵tan∠DAC=![]() =
=![]() =
=![]() ,∴tan∠B=
,∴tan∠B=![]() =
=![]() ,
,
∴BC=12,
∴BD=9,AB=![]() =6
=6![]() .
.


 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行2000米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC,支架AB高1.2米,大门打开的宽度BC为2米,以下哪辆车可以通过?(栏杆宽度,汽车反光镜忽略不计)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.车辆尺寸:长×宽×高)( )
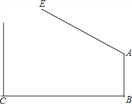
A. 宝马Z4(4200mm×1800mm×1360mm) B. 奔驰smart(4000mm×1600mm×1520mm)
C. 大众朗逸(4600mm×1700mm×1400mm) D. 奥迪A6L(4700mm×1800mm×1400mm)
查看答案和解析>>
科目:初中数学 来源: 题型:
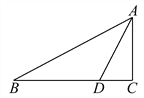
【题目】如图,已知在Rt△ABC中,∠C=90°,D是BC边上一点,AC=6,CD=3,∠ADC=α.
(1)试写出α的正弦、余弦、正切这三个函数值;
(2)若∠B与∠ADC互余,求BD及AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习“利用三角函数测高”后,某综合实践活动小组实地测量了凤凰山与中心广场的相对高度AB,其测量步骤如下:
(1)在中心广场测点C处安置测倾器,测得此时山顶A的仰角∠AFH=30°;
(2)在测点C与山脚B之间的D处安置测倾器(C、D与B在同一直线上,且C、D之间的距离可以直接测得),测得此时山顶上红军亭顶部E的仰角∠EGH=45°;
(3)测得测倾器的高度CF=DG=1.5米,并测得CD之间的距离为288米;
已知红军亭高度为12米,请根据测量数据求出凤凰山与中心广场的相对高度AB.(![]() 取1.732,结果保留整数)
取1.732,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
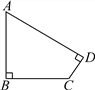
【题目】如图所示,在四边形ABCD中,∠B=∠D=90°,AB=BC=15千米,CD=3![]() 千米.求四边形ABCD的周长和面积(结果保留整数,参考数据:
千米.求四边形ABCD的周长和面积(结果保留整数,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45).
≈2.45).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陈老师为学校购买运动会的奖品后,回学校向后勤处王老师交账说:“我买了两种书,共105本,单价分别为8元和12元,买书前我领了1500元,现在还余418元.”王老师算了一下,说:“你肯定搞错了.”
(1)王老师为什么说他搞错了?试用方程的知识给予解释;
(2)陈老师连忙拿出购物发票,发现的确弄错了,因为他还买了一个笔记本.但笔记本的单价已模糊不清,只能辨认出应为小于10元的整数,笔记本的单价可能为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
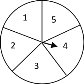
【题目】如图,转盘中5个扇形的面积都相等,任意转动转盘一次,当转盘停止转动时,把下列事件:①指针落在标有3的区域内;②指针落在标有奇数的区域;③指针落在标有6的区域内;④指针落在标有偶数或奇数的区域,的序号按发生的可能性从小到大的顺序排列为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了深化瑶海教育改革发展,办好人民满意的教育,自![]() 年以来,瑶海区加大了教育经费的投入,
年以来,瑶海区加大了教育经费的投入,![]() 年该区投入教育经费
年该区投入教育经费![]() 万元,
万元,![]() 年投入教育经费
年投入教育经费![]() 万元,假设该区这两年投入教育经费的年平均增长率相同.
万元,假设该区这两年投入教育经费的年平均增长率相同.
(1)求这两年该县投入教育经费的年平均增长率;
(2)若该县教育经费的投入还将保持相同的年平均增长率,请你预算![]() 年该区投入教育经费多少万元.
年该区投入教育经费多少万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com