
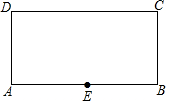
 如图,点E为矩形ABCD边AB的中点,连接CE,作射线DE,若点F为矩形ABCD边上任意一点,沿EF将矩形折叠,使点A恰好落在射线DE上,已知AD=2,CD=4.则DF=4-2$\sqrt{2}$或3$\sqrt{2}$.
如图,点E为矩形ABCD边AB的中点,连接CE,作射线DE,若点F为矩形ABCD边上任意一点,沿EF将矩形折叠,使点A恰好落在射线DE上,已知AD=2,CD=4.则DF=4-2$\sqrt{2}$或3$\sqrt{2}$. 分析 分两种情形:①当EF平分∠AED时,点A恰好落在射线DE上,作FH⊥DE于H.②当EF′平分∠DEB时,点A恰好落在射线DE上,分别求解即可.
解答 解:如图,①当EF平分∠AED时,点A恰好落在射线DE上,作FH⊥DE于H.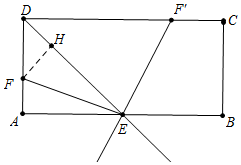
∵AD=AE=2,∠A=90°,
∴∠ADE=∠AED=45°,
∴DH=FA=AF,设AF=FH=DH=x,则DF=$\sqrt{2}$x,
∴x+$\sqrt{2}$x=2,
∴x=2$\sqrt{2}$-2,
∴DF=4-2$\sqrt{2}$.
②当EF′平分∠DEB时,点A恰好落在射线DE上,
∵CD∥AB,
∴∠DF′E=∠F′EB=∠DEF′,
∴DF′=DE=3$\sqrt{2}$,
综上所述,满足条件的DF的长为4-2$\sqrt{2}$或3$\sqrt{2}$.
点评 本题考查翻折变换、矩形的性质、等腰三角形的判定、等腰直角三角形的性质和判定、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考填空题中的压轴题.


科目:初中数学 来源: 题型:选择题
| A. | 15500(1+x)2=13000 | B. | 15500(1-x)2=13000 | C. | 13000(1+x)2=15500 | D. | 13000(1-x)2=15500 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
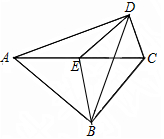 如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD.若∠BAD=58°,则∠EBD的度数为32度.
如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD.若∠BAD=58°,则∠EBD的度数为32度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
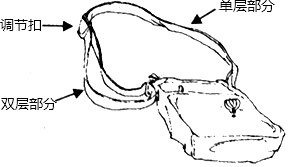 如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:| 单层部分的长度x(cm) | … | 4 | 6 | 8 | 10 | … | 150 |
| 双层部分的长度y(cm) | … | 73 | 72 | 71 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -2 | -1 | 0 | 1 | 1.4 | 2.4 | 2.5 | 3 | 4 | 5 | … |
| y | … | -3.25 | -2.33 | -1.50 | -1 | -1.27 | 3.9 | 3.5 | 3 | m | 4.33 | … |
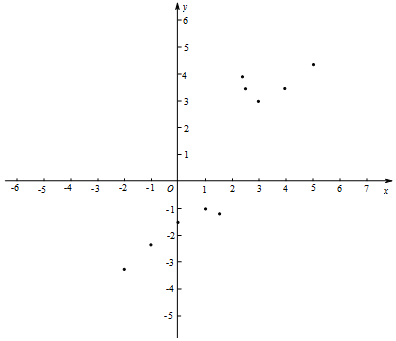
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
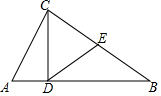 如图,△ABC中,E为BC边的中点,CD⊥AB,AB=2,AC=1,DE=$\frac{\sqrt{3}}{2}$,则∠CDE+∠ACD=( )
如图,△ABC中,E为BC边的中点,CD⊥AB,AB=2,AC=1,DE=$\frac{\sqrt{3}}{2}$,则∠CDE+∠ACD=( )| A. | 60° | B. | 75° | C. | 90° | D. | 105° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 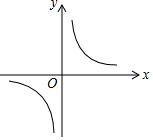 | B. | 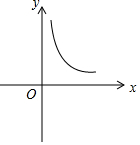 | ||
| C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com