
【题目】如图,将矩形ABCD沿对角线AC翻折,点B落在点E处,EC交AD于F.
(1)求证:△AEF≌△CDF;
(2)若AB=4,BC=8,EF=3,求图中阴影部分的面积。

【答案】(1)见解析;(2)10.
【解析】(1)根据矩形性质和折叠性质可得:∠E=∠D,∠AFE=∠CFD,AE=CD,
故△AEF≌△CDF(AAS);
(2)结合(1)可得阴影部分的面积=S△ADC-S△FDC=![]() AD·DC-
AD·DC-![]() FD·DC,代入已知数可得.
FD·DC,代入已知数可得.
解:(1)∵四边形ABCD是矩形,
∴AB=CD,∠B=∠D=90,
∵将矩形ABCD沿对角线AC翻折,点B落在点E处,
∴∠E=∠B,AB=AE,
∴AE=CD,∠E=∠D,
在△AEF与△CDF中,
∠E=∠D,∠AFE=∠CFD,AE=CD,
∴△AEF≌△CDF(AAS);
(2)根据(1)得:△AEF≌△CDF,EF=3
∴DF=EF=3
∵AB=4,BC=8,
∴AD=BC=8, CD=AB=4
∴阴影部分的面积=S△ADC-S△FDC=![]() AD·DC-
AD·DC-![]() FD·DC
FD·DC
=![]() ×8×4-
×8×4-![]() ×3×4
×3×4
=16-6=10


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2(如图(2));正方形A2B2C2D2的面积为________,以此下去…,则正方形AnBnCnDn的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图,在四边形ABCD中,AD∥BC,点E在BC的延长线上,CE=BC,连接AE,交CD边于点F,且CF=DF.(1)求证:AD=BC;(2)连接BD、DE,若BD⊥DE,求证:四边形ABCD为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,第3次输出的结果是 ,依次继续下去…,第2013次输出的结果是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AEF,延长EF交边BC于点G,连结AG,CF,则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤S△FGC=![]() ;其中正确的结论有_____.
;其中正确的结论有_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
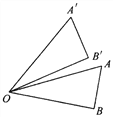
【题目】如图,Rt△AOB绕着一点旋转到△A′OB′的位置,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段和角.已知∠AOB=30°,∠AOB′=10°,那么点B的对应点是点______;线段OB的对应线段是线段_____;∠A的对应角是______;旋转中心是点_______;旋转的角度是______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小强上山游玩,小颖乘坐缆车,小强步行,两人相约在山顶的缆车终点会和,已知小强行走到缆车终点的路程是缆车到山顶的线路长的![]() 倍,小颖在小强出发后
倍,小颖在小强出发后![]() 分才乘上缆车,缆车的平均速度为
分才乘上缆车,缆车的平均速度为![]() 米/分,若图中的折线表示小强在整个行走过程中的路程(米)与出发时间(分)之间的关系的图像,请回答下列问题.
米/分,若图中的折线表示小强在整个行走过程中的路程(米)与出发时间(分)之间的关系的图像,请回答下列问题.

(1)小强行走的总路程是 米,他途中休息了 分;
(2)分别求出小强在休息前和休息后所走的两段路程的速度;
(3)当小颖到达缆车终点时,小强离缆车终点的路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A,B,C,D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2-2x-3,AB为半圆的直径,则这个“果圆”被y轴截得的弦CD的长为____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com