дФЖСвдЯТЕФВФСЯЃК
ШчЙћСНИіе§Ъ§aЃЌbЃЌМДa>0ЃЌb>0ЃЌгаЯТУцЕФВЛЕШЪНЃК
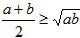
ЕБЧвНіЕБa=bЪБШЁЕНЕШКХЃЌЮвУЧАб
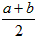
Назіе§Ъ§ЕФЫуЪѕЦНОљЪ§ЃЌАб
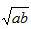
Назіе§Ъ§aЃЌbЕФМИКЮЦНОљЪ§ЃЌгкЪЧЩЯЪіВЛЕШЪНПЩБэЪіЮЊЃКСНИіе§Ъ§ЕФЫуЪѕЦНОљЪ§ВЛаЁгкЃЈМДДѓгкЛђЕШгкЃЉЫќУЧЕФМИКЮЦНОљЪ§ЁЃЫќдкЪ§бЇжагаЙуЗКЕФгІгУЃЌЪЧНтОізюжЕЮЪЬтЕФгаСІЙЄОпЁЃЯТУцОйвЛР§згЃК
Р§ЃКвбжЊx>0ЃЌЧѓКЏЪ§
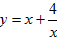
ЕФзюаЁжЕЁЃ
НтЃКСюa=xЃЌ
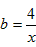
ЃЌдђга
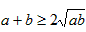
ЃЌЕУ
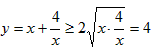
ЃЌЕБЧвНіЕБ
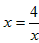
ЪБЃЌМДx=2ЪБЃЌКЏЪ§газюаЁжЕЃЌзюаЁжЕЮЊ2ЁЃ
ИљОнЩЯУцЛиД№ЯТСаЮЪЬтЃК
ЂйвбжЊx>0ЃЌдђЕБx=______ЪБЃЌКЏЪ§
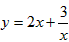
ШЁЕНзюаЁжЕЃЌзюаЁжЕЮЊ______ЃЛ
ЂкгУРщАЪЮЇвЛИіУцЛ§ЮЊ100m
2ЕФОиаЮЛЈдАЃЌЮЪетИіОиаЮЕФГЄЁЂПэИїЮЊЖрЩйЪБЃЌЫљгУЕФРщАЪзюЖЬЃЌзюЖЬЕФРщАЪжмГЄЪЧЖрЩйЃЛ
ЂлвбжЊx>0ЃЌдђздБфСПxШЁКЮжЕЪБЃЌКЏЪ§
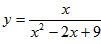
ШЁЕНзюДѓжЕЃЌзюДѓжЕЮЊЖрЩйЃП

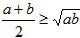 ЕБЧвНіЕБa=bЪБШЁЕНЕШКХЃЌЮвУЧАб
ЕБЧвНіЕБa=bЪБШЁЕНЕШКХЃЌЮвУЧАб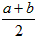 Назіе§Ъ§ЕФЫуЪѕЦНОљЪ§ЃЌАб
Назіе§Ъ§ЕФЫуЪѕЦНОљЪ§ЃЌАб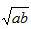 Назіе§Ъ§aЃЌbЕФМИКЮЦНОљЪ§ЃЌгкЪЧЩЯЪіВЛЕШЪНПЩБэЪіЮЊЃКСНИіе§Ъ§ЕФЫуЪѕЦНОљЪ§ВЛаЁгкЃЈМДДѓгкЛђЕШгкЃЉЫќУЧЕФМИКЮЦНОљЪ§ЁЃЫќдкЪ§бЇжагаЙуЗКЕФгІгУЃЌЪЧНтОізюжЕЮЪЬтЕФгаСІЙЄОпЁЃЯТУцОйвЛР§згЃК
Назіе§Ъ§aЃЌbЕФМИКЮЦНОљЪ§ЃЌгкЪЧЩЯЪіВЛЕШЪНПЩБэЪіЮЊЃКСНИіе§Ъ§ЕФЫуЪѕЦНОљЪ§ВЛаЁгкЃЈМДДѓгкЛђЕШгкЃЉЫќУЧЕФМИКЮЦНОљЪ§ЁЃЫќдкЪ§бЇжагаЙуЗКЕФгІгУЃЌЪЧНтОізюжЕЮЪЬтЕФгаСІЙЄОпЁЃЯТУцОйвЛР§згЃК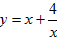 ЕФзюаЁжЕЁЃ
ЕФзюаЁжЕЁЃ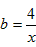 ЃЌдђга
ЃЌдђга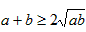 ЃЌЕУ
ЃЌЕУ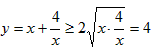 ЃЌЕБЧвНіЕБ
ЃЌЕБЧвНіЕБ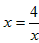 ЪБЃЌМДx=2ЪБЃЌКЏЪ§газюаЁжЕЃЌзюаЁжЕЮЊ2ЁЃ
ЪБЃЌМДx=2ЪБЃЌКЏЪ§газюаЁжЕЃЌзюаЁжЕЮЊ2ЁЃ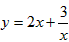 ШЁЕНзюаЁжЕЃЌзюаЁжЕЮЊ______ЃЛ
ШЁЕНзюаЁжЕЃЌзюаЁжЕЮЊ______ЃЛ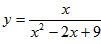 ШЁЕНзюДѓжЕЃЌзюДѓжЕЮЊЖрЩйЃП
ШЁЕНзюДѓжЕЃЌзюДѓжЕЮЊЖрЩйЃП 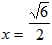 ЃЌКЏЪ§
ЃЌКЏЪ§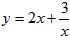 ШЁЕНзюаЁжЕЃЌзюаЁжЕЮЊ
ШЁЕНзюаЁжЕЃЌзюаЁжЕЮЊ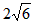 ЃЛ
ЃЛ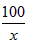 УзЃЌЫљгУЕФРщАЪзмГЄЮЊyУзЃЌИљОнЬтвтЕУЃК
УзЃЌЫљгУЕФРщАЪзмГЄЮЊyУзЃЌИљОнЬтвтЕУЃК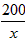 ЃЌ
ЃЌ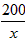 Ён40ЃЌ
Ён40ЃЌ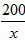 ЃЌ
ЃЌ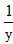 =
=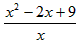 =x+
=x+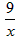 -2
-2 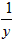 =x+
=x+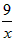 Ён6ЃЌ
Ён6ЃЌ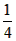 ЁЃ
ЁЃ

 МЄЛюЫМЮЌгХМгПЮЬУЯЕСаД№АИ
МЄЛюЫМЮЌгХМгПЮЬУЯЕСаД№АИ ЛюСІЪдОэЯЕСаД№АИ
ЛюСІЪдОэЯЕСаД№АИ
 x-2ЃЉ2+
x-2ЃЉ2+ ______ЃЎ
______ЃЎ