
【题目】如图,直线y=x+m与y=nx﹣5n(n≠0)的交点的横坐标为3,则关于x的不等式x+m>nx﹣5n>0的整数解为( )
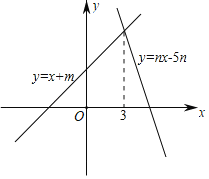
A.3B.4C.5D.6
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
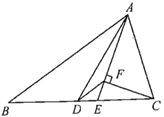
【题目】如图所示,在![]() 中,AB>AC,AD是中线,AE是角平分线,CF⊥AE于点F,连接DF,则①DF//AB;②∠DAE=
中,AB>AC,AD是中线,AE是角平分线,CF⊥AE于点F,连接DF,则①DF//AB;②∠DAE=![]() (∠ACB-∠ABC);③DF=
(∠ACB-∠ABC);③DF=![]() (AB-AC);④
(AB-AC);④![]() (AB-AC)<AD<
(AB-AC)<AD<![]() (AB+AC).其中正确的是__________.
(AB+AC).其中正确的是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.《九章算术》中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”
译文:“今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕毎只各重多少斤?”
设每只雀重x斤,每只燕重y斤,可列方程组为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ACB=90°,AC > BC,CD是Rt△ABC的高,E是AC的中点,ED的延长线与CB的延长线相交于点F.
(1)求证:DF是BF和CF的比例中项;
(2)在AB上取一点G,如果AE·AC=AG·AD,求证:EG·CF=ED·DF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
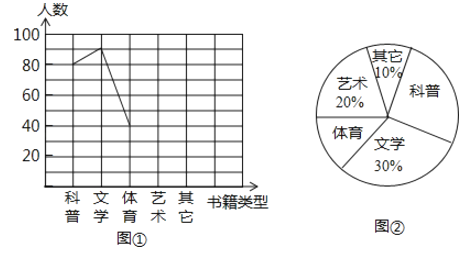
(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;
(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;
(4)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+mx+n与直线y=﹣
x2+mx+n与直线y=﹣![]() x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
(1)求抛物线的关系式和tan∠BAC的值;
(2)P为抛物线上一动点,连接PA,过点P作PQ⊥OA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ACB相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)在AB上找一点M,使得OM+DM的值最小,直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() ,
,![]() 的平分线分别交
的平分线分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点,
两点,![]() 为
为![]() 的中点,
的中点,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,连接
,连接![]() ,下列结论:①
,下列结论:①![]() 为等腰三角形;②
为等腰三角形;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有( )
.其中正确的结论有( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
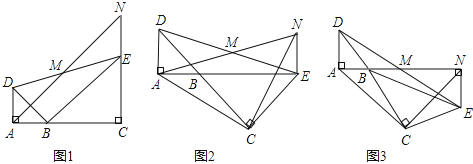
【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组开展了一次活动,过程如下:设![]() .现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线
.现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线![]() 、
、![]() 上.
上.
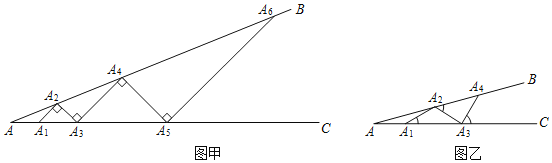
活动一、如图甲所示,从点![]() 开始,依次向右摆放小棒,使小棒与小棒在端点处互相垂直(
开始,依次向右摆放小棒,使小棒与小棒在端点处互相垂直(![]() 为第1根小棒)
为第1根小棒)
数学思考:
(1)小棒能无限摆下去吗?答: (填“能”或“不能”)
(2)设![]() ,求
,求![]() 的度数;
的度数;
活动二:如图乙所示,从点![]() 开始,用等长的小棒依次向右摆放,其中
开始,用等长的小棒依次向右摆放,其中![]() 为第一根小棒,且
为第一根小棒,且![]() .
.
数学思考:
(3)若已经摆放了3根小棒,则![]() ,
,![]() ,
,![]() ;(用含
;(用含![]() 的式子表示)
的式子表示)
(4)若只能摆放5根小棒,则![]() 的取值范围是 .
的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com