
 如图,矩形ABCD,AB=1,BC=2,点O为BC中点,弧AD的圆心为O,则阴影部分面积为$\frac{π}{2}$.
如图,矩形ABCD,AB=1,BC=2,点O为BC中点,弧AD的圆心为O,则阴影部分面积为$\frac{π}{2}$. 分析 连接OA、OD,根据题意得到△AOB和△DOC是等腰直角三角形,求得OA=OD=$\sqrt{2}$,进而求得∴∠AOD=90°,根据三角形的面积公式求得S△ABD=S△AOD,然后根据扇形的面积公式计算即可.
解答 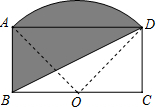 解:连接OA、OD,
解:连接OA、OD,
∵矩形ABCD,AB=1,BC=2,点O为BC中点,
∴OB=OC=1,
∴AB=OB=OC=DC=1,
∴△AOB和△DOC是等腰直角三角形,
∴∠AOB=45°=∠DOC,OA=OD=$\sqrt{2}$,
∴∠AOD=90°,
∵S△ABD=$\frac{1}{2}$AD•AB=S△AOD,
∴S阴影=S扇形AOD=$\frac{90π×(\sqrt{2})^{2}}{360}$=$\frac{π}{2}$,
故答案为:$\frac{π}{2}$.
点评 本题考查的是扇形的面积计算,掌握矩形的性质、等腰直角三角形的性质和扇形的面积公式S=$\frac{nπ{R}^{2}}{360}$是解题的关键.


科目:初中数学 来源: 题型:解答题
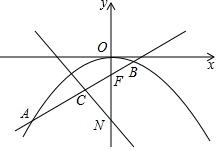 如图,过F(0,-1)的直线y=kx+b(k≠0)与抛物线y=-$\frac{1}{4}$x2交于A(x1,y1),B(x2,y2)两点.
如图,过F(0,-1)的直线y=kx+b(k≠0)与抛物线y=-$\frac{1}{4}$x2交于A(x1,y1),B(x2,y2)两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
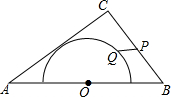 如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最小值是1.
如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最小值是1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -8 | B. | 6 | C. | -5 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
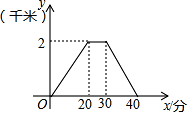 某天,小王去朋友家借书,在朋友家停留一段时间后,返回家中,如图是他离家的路程y(千米)与时间x(分)关系的图象,根据图象信息,下列说法正确的是( )
某天,小王去朋友家借书,在朋友家停留一段时间后,返回家中,如图是他离家的路程y(千米)与时间x(分)关系的图象,根据图象信息,下列说法正确的是( )| A. | 小王去时的速度大于回家的速度 | |
| B. | 小王去时走上坡路,回家时走下坡路 | |
| C. | 小王去时所花时间少于回家所花时间 | |
| D. | 小王在朋友家停留了10分 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com