
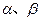 ,且测得AB=a米。
,且测得AB=a米。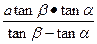
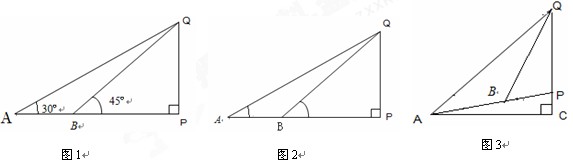
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源:不详 题型:解答题
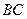 、
、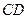 上有动点
上有动点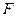 、
、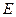 ,点
,点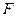 以每秒
以每秒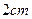 的速度,在线段
的速度,在线段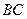 上从点B向点C匀速运动;同时点
上从点B向点C匀速运动;同时点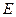 以每秒
以每秒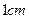 的速度,在线段
的速度,在线段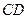 上从点C向点D匀速运动.当点
上从点C向点D匀速运动.当点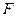 到达点C时,点
到达点C时,点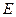 同时停止运动.设点
同时停止运动.设点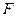 运动的时间为t(秒).
运动的时间为t(秒). ,求y 关于t的函数关系式,并写出函数定义域;
,求y 关于t的函数关系式,并写出函数定义域;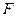 、
、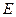 在运动过程中,如
在运动过程中,如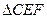 与
与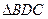 相似,求线段
相似,求线段 的长.
的长.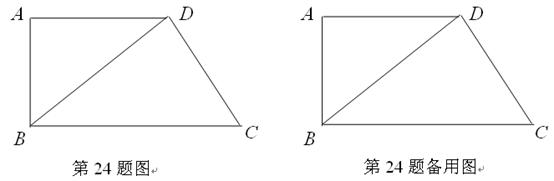
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
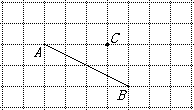
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
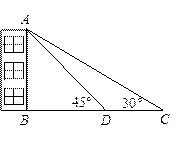
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,金属丝就缩短0.002mm.把15℃的这种金属丝加热到50℃,再冷却降温到8℃,金属丝最后的长度比原来的长度伸长多少?
,金属丝就缩短0.002mm.把15℃的这种金属丝加热到50℃,再冷却降温到8℃,金属丝最后的长度比原来的长度伸长多少?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com