
ЁОЬтФПЁПвбжЊOЮЊжБЯпMNЩЯвЛЕуЃЌOPЁЭMNЃЌдкЕШбќRtЁїABOжаЃЌ ![]() ЃЌACЁЮOPНЛOMгкCЃЌDЮЊOBЕФжаЕуЃЌDEЁЭDCНЛMNгкEЃЎ
ЃЌACЁЮOPНЛOMгкCЃЌDЮЊOBЕФжаЕуЃЌDEЁЭDCНЛMNгкEЃЎ
(1) ШчЭМ1ЃЌШєЕуBдкOPЩЯЃЌдђЂйAC OE(ЬюЁАЃМЁБЃЌЁАЃНЁБЛђЁАЃОЁБ)ЃЛЂкЯпЖЮCAЁЂCOЁЂCDТњзуЕФЕШСПЙиЯЕЪНЪЧ ЃЛ
(2) НЋЭМ1жаЕФЕШбќRtЁїABOШЦOЕуЫГЪБеыа§зЊ(![]() )ЃЌШчЭМ2ЃЌФЧУД(1)жаЕФНсТлЂкЪЧЗёГЩСЂЃПЧыЫЕУїРэгЩЃЛ
)ЃЌШчЭМ2ЃЌФЧУД(1)жаЕФНсТлЂкЪЧЗёГЩСЂЃПЧыЫЕУїРэгЩЃЛ
(3) НЋЭМ1жаЕФЕШбќRtЁїABOШЦOЕуЫГЪБеыа§зЊ()ЃЌЧыФудкЭМ3жаЛГіЭМаЮЃЌВЂжБНгаДГіЯпЖЮCAЁЂCOЁЂCDТњзуЕФЕШСПЙиЯЕЪН ЃЛ
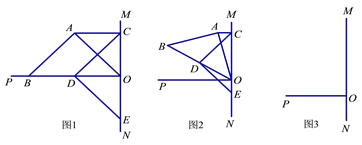
ЁОД№АИЁПЃЈ1ЃЉЂй=ЃЛЂкAC2+CO2=CD2ЃЛЃЈ2ЃЉЃЈ1ЃЉжаЕФНсТлЂкВЛГЩСЂЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉЛЭММћНтЮіЃЛOC-CA=![]() CD.
CD.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЂйШчЭМ1ЃЌжЄУїAC=OCКЭOC=OEПЩЕУНсТлЃЛЂкИљОнЙДЙЩЖЈРэПЩЕУЃКAC2+CO2=CD2ЃЛЃЈ2ЃЉШчЭМ2ЃЌЃЈ1ЃЉжаЕФНсТлЂкВЛГЩСЂЃЌзїИЈжњЯпЃЌЙЙНЈШЋЕШШ§НЧаЮЃЌжЄУїAЁЂDЁЂOЁЂCЫФЕуЙВдВЃЌЕУЁЯACD=ЁЯAOBЃЌЭЌРэЕУЃКЁЯEFO=ЁЯEDOЃЌдйжЄУїЁїACOЁеЁїEOFЃЌЕУOE=ACЃЌAO=EFЃЌИљОнЙДЙЩЖЈРэЕУЃКAC2+OC2=FO2+OE2=EF2ЃЌгЩжБНЧШ§НЧаЮжазюГЄБпЮЊаББпПЩЕУНсТлЃЛЃЈ3ЃЉШчЭМ3ЃЌСЌНгADЃЌдђAD=ODжЄУїЁїACDЁеЁїOEDЃЌИљОнЁїCDEЪЧЕШбќжБНЧШ§НЧаЮЃЌЕУCE2=2CD2ЃЌЕШСПДњЛЛПЩЕУНсТлЃЈOCЉOEЃЉ2=ЃЈOCЉACЃЉ2=2CD2ЃЌПЊЗНКѓЪЧЃКOCЉAC=![]() CDЃЎ
CDЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЂйAC=OEЃЌ
РэгЩЃКШчЭМ1ЃЌЁпдкЕШбќRtЁїABOжаЃЌЁЯBAO=90ЁуЃЌЁрЁЯABO=ЁЯAOB=45ЁуЃЌ
ЁпOPЁЭMNЃЌЁрЁЯCOP=90ЁуЃЌЁрЁЯAOC=45ЁуЃЌ
ЁпACЁЮOPЃЌЁрЁЯCAO=ЁЯAOB=45ЁуЃЌЁЯACO=ЁЯPOE=90ЁуЃЌЁрAC=OCЃЌ
СЌНгADЃЌ
ЁпBD=ODЃЌЁрAD=ODЃЌADЁЭOBЃЌЁрADЁЮOCЃЌЁрЫФБпаЮADOCЪЧе§ЗНаЮЃЌЁрЁЯDCO=45ЁуЃЌ
ЁрAC=ODЃЌЁрЁЯDEO=45ЁуЃЌЁрCD=DEЃЌЁрOC=OEЃЌ
ЁрAC=OEЃЛ
ЂкдкRtЁїCDOжаЃЌ
ЁпCD2=OC2+OD2ЃЌЁрCD2=AC2+OC2ЃЛ
ЙЪД№АИЮЊЃКAC2+CO2=CD2ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЃЈ1ЃЉжаЕФНсТлЂкВЛГЩСЂЃЌ
РэгЩЪЧЃК
СЌНгADЃЌбгГЄCDНЛOPгкFЃЌСЌНгEFЃЌ
ЁпAB=AOЃЌDЮЊOBЕФжаЕуЃЌЁрADЁЭOBЃЌЁрЁЯADO=90ЁуЃЌ
ЁпЁЯCDE=90ЁуЃЌЁрЁЯADO=ЁЯCDEЃЌЁрЁЯADOЉЁЯCDO=ЁЯCDEЉЁЯCDOЃЌМДЁЯADC=ЁЯEDOЃЌ
ЁпЁЯADO=ЁЯACO=90ЁуЃЌЁрЁЯADO+ЁЯACO=180ЁуЃЌЁрAЁЂDЁЂOЁЂCЫФЕуЙВдВЃЌЁрЁЯACD=ЁЯAOBЃЌ
ЭЌРэЕУЃКЁЯEFO=ЁЯEDOЃЌЁрЁЯEFO=ЁЯAOCЃЌ
ЁпЁїABOЪЧЕШбќжБНЧШ§НЧаЮЃЌЁрЁЯAOB=45ЁуЃЌЁрЁЯDCO=45ЁуЃЌЁрЁїCOFКЭЁїCDEЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрOC=OFЃЌЁпЁЯACO=ЁЯEOF=90ЁуЃЌЁрЁїACOЁеЁїEOFЃЌЁрOE=ACЃЌAO=EFЃЌЁрAC2+OC2=FO2+OE2=EF2ЃЌ
RtЁїDEFжаЃЌEFЃОDE=DCЃЌЁрAC2+OC2ЃОDC2ЃЌ
ЫљвдЃЈ1ЃЉжаЕФНсТлЂкВЛГЩСЂЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌНсТлЃКOCЉCA=![]() CDЃЌ
CDЃЌ
РэгЩЪЧЃКСЌНгADЃЌдђAD=ODЃЌ
ЭЌРэЃКЁЯADC=ЁЯEDOЃЌ
ЁпЁЯCAB+ЁЯCAO=ЁЯCAO+ЁЯAOC=90ЁуЃЌЁрЁЯCAB=ЁЯAOCЃЌ
ЁпЁЯDAB=ЁЯAOD=45ЁуЃЌЁрЁЯDABЉЁЯCAB=ЁЯAODЉЁЯAOCЃЌ
МДЁЯDAC=ЁЯDOEЃЌЁрЁїACDЁеЁїOEDЃЌЁрAC=OEЃЌCD=DEЃЌЁрЁїCDEЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрCE2=2CD2ЃЌЁрЃЈOCЉOEЃЉ2=ЃЈOCЉACЃЉ2=2CD2ЃЌЁрOCЉAC=![]() CDЃЌ
CDЃЌ
ЙЪД№АИЮЊЃКOCЉAC=![]() CDЃЎ
CDЃЎ






| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП НЋХзЮяЯпy=x2-2xЯђЩЯЦНвЦ3ИіЕЅЮЛЃЌдйЯђгвЦНвЦ4ИіЕЅЮЛЕУЕНЕФХзЮяЯпНтЮіЪНЮЊ .
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпy=![]() xЉ6ЗжБ№НЛxжсЃЌyжсгкAЃЌBЃЌMЪЧЗДБШР§КЏЪ§y=
xЉ6ЗжБ№НЛxжсЃЌyжсгкAЃЌBЃЌMЪЧЗДБШР§КЏЪ§y=![]() ЃЈxЃО0ЃЉЕФЭМЯѓЩЯЮЛгкжБЯпЩЯЗНЕФвЛЕуЃЌMCЁЮxжсНЛABгкCЃЌMDЁЭMCНЛABгкDЃЌACBD=4
ЃЈxЃО0ЃЉЕФЭМЯѓЩЯЮЛгкжБЯпЩЯЗНЕФвЛЕуЃЌMCЁЮxжсНЛABгкCЃЌMDЁЭMCНЛABгкDЃЌACBD=4![]() ЃЌдђkЕФжЕЮЊЃЈ ЃЉ
ЃЌдђkЕФжЕЮЊЃЈ ЃЉ
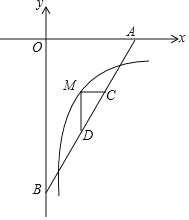
AЃЎЉ3 BЃЎЉ4 CЃЎЉ5 DЃЎЉ6
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊABЁЮCDЃЌBEЦНЗжЁЯABCЃЌDEЦНЗжЁЯADCЃЌЁЯBAD=80ЁуЃЌЪдЧѓЃК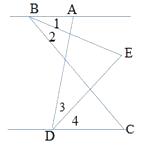
ЃЈ1ЃЉЁЯEDCЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШєЁЯBCD=nЁуЃЌЪдЧѓЁЯBEDЕФЖШЪ§ЁЃ(гУКЌnЕФЪНзгБэЪОЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПУќЬтЁАСНИіШёНЧжЎКЭвЛЖЈЪЧЖлНЧЁБЪЧ_____ЃЎЃЈЬюЁАецУќЬтЁБЛђЁАМйУќЬтЁБЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬтЪЧецУќЬтЕФЪЧЃЈ ЃЉ
A.ДЙЯпЖЮзюЖЬ
B.ЭЌХдФкНЧЛЅВЙ
C.ШчЙћСНИіЪЕЪ§ЕФОјЖджЕЯрЕШЃЌФЧУДетСНИіЪЕЪ§ЯрЕШ
D.вЛИіНЧЕФСНБпгыСэвЛИіНЧЕФСНБпЗжБ№ЦНааЃЌФЧУДетСНИіНЧЯрЕШ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкxжсЩЯгаЕуP(aЃЌ0)ЃЈЦфжаa>2)ЃЌЙ§ЕуPзїxаБЕФХюЯпЃЌЗжБ№НЛКЏЪ§ ![]() КЭ
КЭ ![]() ЕФЭМЯѓгкЕуCЁЂDЁЃ
ЕФЭМЯѓгкЕуCЁЂDЁЃ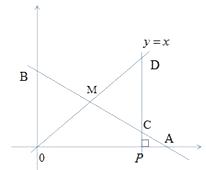
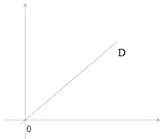
ЃЈ1ЃЉЧѓЕуAЕФзјБъ
ЃЈ2ЃЉШєOB=CDЃЌЧѓaЕФжЕ
ЃЈ3ЃЉдк(2)ЬѕМўЯТШєвд0DЯпЖЮЮЊБпЃЌзїе§ЗНаЮ0DEFЃЌЧѓжБЯпEFЕФБэДяЪНЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаМЦЫуе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A.2x3ЃЈЉ3x2ЃЉ=Љ6x6
B.2a24a2=8a2
C.ЃЈa+bЃЉЃЈbЉaЃЉ=a2Љb2
D.ЃЈ2a2b3ЃЉ23a2b=12a6b7
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЕШБпЁїABCжаЃЌAOЪЧИпЃЌDЮЊAOЩЯвЛЕуЃЌвдCDЮЊвЛБпЃЌдкCDЯТЗНзїЕШБпЁїCDEЃЌСЌНгBE.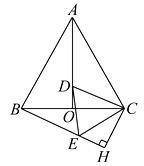
ЃЈ1ЃЉЧѓжЄЃКAD=BEЃЛ
ЃЈ2ЃЉЙ§ЕуCзїCHЁЭBEЃЌНЛBEЕФбгГЄЯпгкHЃЌШєBCЃН8ЃЌЧѓCHЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com