
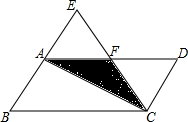
 如图,在平行四边形ABCD中,BC=6cm,将△ABC沿对角线AC折叠,点B的对应点落在点E处,BC边的对应边CE与AD边交于点F,此时△CDF为等边三角形.
如图,在平行四边形ABCD中,BC=6cm,将△ABC沿对角线AC折叠,点B的对应点落在点E处,BC边的对应边CE与AD边交于点F,此时△CDF为等边三角形.分析 (1)首先根据等边三角形的性质可得DF=DC=FC,∠D=60°,根据折叠的性质,∠BCA=∠ECA,再利用平行四边形的性质证明∠DAC=30°,∠ACD=90°,利用直角三角形30°角所对的边等于斜边的一半可得CD长,进而可得AB的长;
(2)利用三角函数值计算出AC,然后根据三角形的中线平分三角形的面积可得S△ACF=$\frac{1}{2}$S△ACD,进而可得答案.
解答 解:(1)∵△CDF为等边三角形,
∴DF=DC=FC,∠D=60°,
根据折叠的性质,∠BCA=∠ECA,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=6cm,AB=CD,
∴∠FAC=∠BCA,
∴∠FAC=∠FCA,
∴FA=FC,
∴∠DAC=30°,
∴∠ACD=90°,
∴CD=$\frac{1}{2}$AD=3cm,
∵AB=3cm;
(2)∵CD=3cm,∠ACD=90°,∠DAC=30°,
∴AC=3$\sqrt{3}$cm,
∴S△ACF=$\frac{1}{2}$S△ACD=$\frac{1}{4}$×AC•CD=$\frac{1}{4}$×3×3$\sqrt{3}$=$\frac{9\sqrt{3}}{4}$(cm2).
点评 此题主要考查了平行四边形的性质、直角三角形的性质以及翻折变换,关键是掌握平行四边形的对边平行且相等,直角三角形30°角所对的边等于斜边的一半.


科目:初中数学 来源: 题型:选择题
| A. | 用抽样调查了解广州市中学生每周使用手机所用的时间 | |
| B. | 用全面调查了解某班学生对6月5日是“世界环境日”的知晓情况 | |
| C. | 用抽样调查选出某校短跑最快的学生参加全市比赛 | |
| D. | 用抽样调查了解南沙区初中学生零花钱的情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
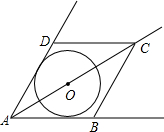 如图,菱形ABCD的边长为2,∠DAB=60°,点 O为射线AC上动点,动圆⊙O始终与射线AB相切,研究⊙O与菱形ABCD各边交点总个数的情况,以下论述正确的是( )
如图,菱形ABCD的边长为2,∠DAB=60°,点 O为射线AC上动点,动圆⊙O始终与射线AB相切,研究⊙O与菱形ABCD各边交点总个数的情况,以下论述正确的是( )| A. | ①②⑤ | B. | ② | C. | ①③④ | D. | ②④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
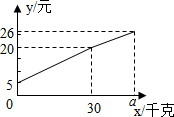 一位农民带上若干千克自产的土豆进城出售.为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示,结合图象回答下列问题:
一位农民带上若干千克自产的土豆进城出售.为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示,结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com