

分析 (1)依据锐角三角函数的定义可求得sin∠PAQ、cos∠PAQ的值;
(2)①过点O作OB⊥AP,垂足为B.依据同角的余角相等可证明∠AOB=∠QAP,然后依据锐角三角函数的定义可求得OB的长;②连接OA′.由切线的性质可知∠OA′A=90°,接下来,依据锐角三角函数的定义可求得AA′的长;
(3)当0<m<2$\sqrt{3}$时,如图3所示:连接OA′,过点O作OH⊥AP,垂足为H.在Rt△OGH中,在Rt△AA′G中,依据锐角三角函数的定义可得到OG=$\frac{\sqrt{39}}{6}$n、GA′=$\frac{\sqrt{3}}{6}$m,然后依据OG+GA′=1可得到n与m之间的函数关系式;当m>2$\sqrt{3}$时,如图2所示,过点O作OH⊥AP,垂足为H,连接A′O并延长交AP与点G.依据锐角三角函数的定义可知OG=$\frac{\sqrt{39}}{6}$n,GA′=$\frac{\sqrt{3}}{6}$m,由GA′-OG=1可得到n与m之间的函数关系式;接下来,依据d和r的关系可求得当直线AP与⊙O相切,相交、相离时m的取值范围.
解答 解:(1)∵∠PAQ的正切值为 $\frac{\sqrt{3}}{6}$,
∴sin∠PAQ=$\frac{\sqrt{3}}{\sqrt{(\sqrt{3})^{2}+{6}^{2}}}$=$\frac{\sqrt{13}}{13}$,cos∠QAQ=$\frac{6}{\sqrt{(\sqrt{3})^{2}+{6}^{2}}}$=$\frac{2\sqrt{39}}{13}$.
故答案为:$\frac{\sqrt{13}}{13}$,$\frac{2\sqrt{39}}{13}$.
(2)①如图1所示:过点O作OB⊥AP,垂足为B.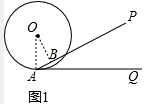
∵AQ是⊙O的切线,
∴OA⊥AQ.
∴∠OAP+∠PAQ=90°.
∵OB⊥AP,
∴∠OAP+∠AOB=90°.
∴∠AOB=∠PAQ.
∴$\frac{OB}{OA}$=cos∠PAQ=$\frac{2\sqrt{39}}{13}$.
∵OA=1,
∴OB=$\frac{2\sqrt{39}}{13}$.
∴圆心O到射线AP的距离为 $\frac{2\sqrt{39}}{13}$.
②如图2所示:连接OA′.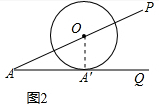
∵⊙O与AQ相切,
∴OA′⊥AQ.
∴∠OA′A=90°.
∴$\frac{OA′}{AA′}$=tan∠A.
∴AA′=2 $\sqrt{3}$.
故答案为:2 $\sqrt{3}$.
(3)当0≤x≤2 $\sqrt{3}$时,如图3所示:连接OA′,过点O作OH⊥AP,垂足为H.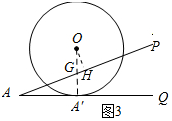
∵在Rt△OGH中,cos∠O=$\frac{OH}{OG}$=$\frac{2\sqrt{39}}{13}$,
∴OG=$\frac{\sqrt{39}}{6}$n.
∵在Rt△AA′G中,tan∠A=$\frac{GA′}{AA′}$=$\frac{\sqrt{3}}{6}$,
∴GA′=$\frac{\sqrt{3}}{6}$m,.
∵OG+GA′=1,
∴$\frac{\sqrt{39}}{6}$n+$\frac{\sqrt{3}}{6}$m=1,.
∴n=-$\frac{\sqrt{13}}{13}$m+$\frac{\sqrt{39}}{39}$.
②当x>2 $\sqrt{3}$时,如图2所示,过点O作OH⊥AP,垂足为H,连接A′O并延长交AP与点G.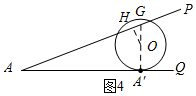
∵∠HGO=∠AGA′,∠GA′A=∠OHD=90°,
∴∠HOG=∠PAQ.
∴OG=$\frac{\sqrt{39}}{6}$n,GA′=$\frac{\sqrt{3}}{6}$m.
由GA′-OG=1得,n=$\frac{\sqrt{13}}{13}$m-$\frac{\sqrt{39}}{39}$.
综上所述,n与m的函数关系式为n=$\left\{\begin{array}{l}{-\frac{\sqrt{13}}{13}m+\frac{\sqrt{39}}{39}}&{(0≤m≤2\sqrt{3})}\\{\frac{\sqrt{13}}{13}m-\frac{\sqrt{39}}{39}}&{(m>2\sqrt{3})}\end{array}\right.$.
∵当n=1时,⊙O与AP相切,此时$\frac{\sqrt{13}}{13}$m-$\frac{\sqrt{39}}{39}$=1,解得m=2$\sqrt{3}$+$\sqrt{13}$,
∴当0≤m<2$\sqrt{3}$+$\sqrt{13}$时,⊙O与AN相交,
当m=2$\sqrt{3}$+$\sqrt{13}$时,⊙O与AN相切;
当m>2$\sqrt{3}$+$\sqrt{13}$时,⊙O与AN相离.
点评 本题主要考查的是圆的综合应用,解答本题主要应用了切线的性质、直线和圆的位置关系、锐角三角函数的定义,依据OA′=1列出n与m的函数关系式是解题的关键.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:解答题
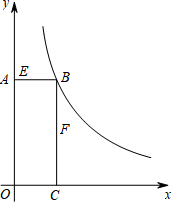 如图,矩形AOCB的顶点B在反比例函数$y=\frac{k}{x}(k>0$,x>0)的图象上,且AB=3,BC=8.若动点E从A开始沿AB向B以每秒1个单位长度的速度运动,同时动点F从B开始沿BC向C以每秒2个单位长度的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动,设运动时间为t秒.
如图,矩形AOCB的顶点B在反比例函数$y=\frac{k}{x}(k>0$,x>0)的图象上,且AB=3,BC=8.若动点E从A开始沿AB向B以每秒1个单位长度的速度运动,同时动点F从B开始沿BC向C以每秒2个单位长度的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com