
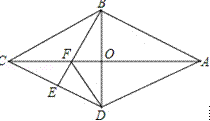
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,AC与BD相交于O点,OC=OA,若E是CD上任意一点,连接BE交AC于点F,连接DF.
(1)证明:△CBF≌△CDF;
(2)若AC=2![]() ,BD=2,求四边形ABCD的周长。
,BD=2,求四边形ABCD的周长。
【答案】(1)证明见解析;(2)四边形ABCD的周长为8.
【解析】试题分析:(1)首先利用SSS定理证明△ABC≌△ADC可得∠BCA=∠DCA即可证明△CBF≌△CDF.
(2) 由△CBF≌△CDF,可知,∠BCF=∠DCF,又CB=CD,得出OB=OD,∠COB=∠COD=90°,因为OC=OA,所以AC与BD互相垂直平分,即可证得四边形ABCD是菱形,然后根据勾股定理全等AB长,进而求得四边形的面积.
试题解析(1)证明:在△ABC和△ADC中, 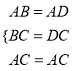 ,
,
∴△ABC≌△ADC(SSS),
∴∠BCA=∠DCA,
在△CBF和△ADF中, 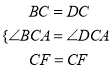 ,
,
∴△CBF≌△CDF(SAS)
(2)∵△CBF≌△CDF,
∴∠BCF=∠DCF,
∴OB=OD,BD⊥AC,
∵OA=OC,
∴四边形ABCD是菱形,
∴AB=BC=CD=DA,
∵AC=2![]() ,BD=2,
,BD=2,
∴OA=![]() ,OB=1,
,OB=1,
∴AB=![]() ,
,
∴四边形ABCD的周长=4AB=4×2=8.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,则点A′的坐标是( )
A.(﹣1,1)
B.(﹣1,﹣2)
C.(﹣1,2)
D.(1,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一条弯曲的公路改成直道,可以缩短路程,其道理用几何知识解释正确的是( )
A.线段可以比较大小
B.线段有两个端点
C.两点之间线段最短
D.过两点有且只有一条直线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线CP是AB的中垂线且交AB于P,其中AP=2CP.甲、乙两人想在AB上取两点D、E,使得AD=DC=CE=EB,其作法如下: 甲:作∠ACP、∠BCP之角平分线,分别交AB于D、E,则D、E即为所求;
乙:作AC、BC之中垂线,分别交AB于D、E,则D、E即为所求.
对于甲、乙两人的作法,下列判断何者正确( )
A.两人都正确
B.两人都错误
C.甲正确,乙错误
D.甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上A、B、C三点对应的数分别是a、b、c,若ab<0,c为最大的负整数,c>a且|b|>|a|.
(1)请在数轴上标出A,B,C三点的大致位置;
(2)化简|a﹣b|+|b﹣a+c|﹣|b﹣c|.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠1=18°18′,∠2=18.18°,∠3=18.3°,下列结论正确的是( )
A.∠1=∠3
B.∠1=∠2
C.∠2=∠3
D.∠1=∠2=∠3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.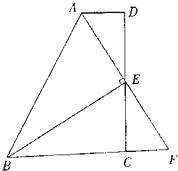
求证:
(1)FC=AD
(2)AB=BC+AD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com