
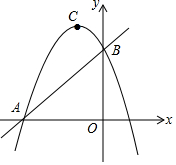
 如图,直线y=x+n与x轴交于点A,与y轴交于点B(点A与点B不重合),抛物线y=-$\frac{1}{2}$x2-2x+c经过点A、B,抛物线的顶点为C.
如图,直线y=x+n与x轴交于点A,与y轴交于点B(点A与点B不重合),抛物线y=-$\frac{1}{2}$x2-2x+c经过点A、B,抛物线的顶点为C.分析 (1)求直线AB与两坐标轴的交点坐标,得OA=OB,可得结论;
(2)如图1,作辅助线,构建直角三角形,证明∠CBA=∠CBD+∠DBA=90°,利用勾股定理计算BC和AB的长,根据正切的定义代入求值即可;
(3)分两种情况:①当点P在CA左侧时,如图2,延长BD交抛物线于点E,此时,点P与点E重合,点P的坐标是(-4,6);
②当点P在CA右侧时,如图3,作辅助线,直线CF与抛物线的交点就是P点.
解答 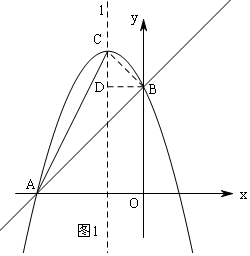 解:(1)y=x+n,
解:(1)y=x+n,
当x=0时,y=n,则B(0,n),
当y=0时,x=-n,则A(-n,0),
∴OA=OB=n,
∴△AOB是等腰直角三角形,
∴∠BAO=45°,
故答案为:45;
(2)由(1)得:B(0,n),A(-n,0),
∵抛物线y=-$\frac{1}{2}$x2-2x+c经过点A、B
∴$\left\{\begin{array}{l}{0=-\frac{1}{2}{n}^{2}+2n+c}\\{c=n}\end{array}\right.$,解得$\left\{\begin{array}{l}{n=6}\\{c=6}\end{array}\right.$或$\left\{\begin{array}{l}{n=0}\\{c=0}\end{array}\right.$(舍去)
∴A(-6,0),B(0,6),直线AB的解析式为:y=x+6,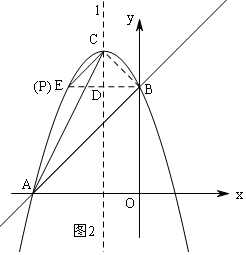
抛物线为:y=-$\frac{1}{2}{x}^{2}$-2x+6=-$\frac{1}{2}$(x+2)2+8,
∴抛物线的顶点为C(-2,8),
设抛物线的对称轴为直线l,连结BC,
如图1,过点B作BD⊥l,则BD=CD=2,BD∥x轴,
∴∠CBD=45°,
又BD∥x轴,
∴∠DBA=∠BAO=45°,
∴∠CBA=∠CBD+∠DBA=90°,
在Rt△CDB中,BC=$\sqrt{C{D}^{2}+B{D}^{2}}$=2$\sqrt{2}$,
在Rt△AOB中,AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=6$\sqrt{2}$,
∴在Rt△ABC中,tan∠CAB=$\frac{BC}{AB}$=$\frac{1}{3}$;
(3)①当点P在CA左侧时,如图2,
延长BD交抛物线于点E,当∠PCA=∠BAC时,CP∥AB,
此时,点P与点E重合,点P的坐标是(-4,6);
②当点P在CA右侧时,如图3,过点A作AC的垂线交CP于点F,
过点A作y轴的平行线m,过点C作CM⊥m,过点F作FN⊥m,
由于tan∠BAC=$\frac{1}{3}$,所以tan∠ACF=tan∠ACP=$\frac{1}{3}$,
∵Rt△CMA∽Rt△ANF,
∴$\frac{AN}{CM}=\frac{AF}{AC}=\frac{1}{3}$,$\frac{NF}{MA}=\frac{AF}{AC}=\frac{1}{3}$,AN=$\frac{1}{3}$CM=$\frac{4}{3}$,NF=$\frac{1}{3}$MA=$\frac{8}{3}$,
∴F(-$\frac{10}{3}$,-$\frac{4}{3}$);
易求得直线CF的解析式为:y=7x+22,
由$\left\{\begin{array}{l}{y=7x+22}\\{y=-\frac{1}{2}{x}^{2}-2x+6}\end{array}\right.$,消去y,得x2+18x+32=0,
解得x=16或x=-2(舍去),
因此点P的坐标(-16,-90);
综上所述,P的坐标是(-4,6)或(-16,-90).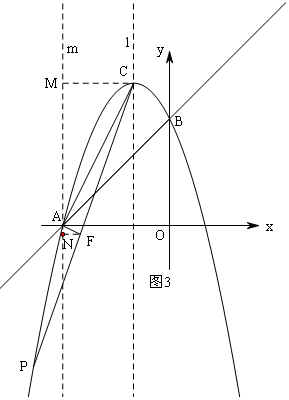
点评 本题是二次函数的综合题,考查了字母系数的函数解析式、与坐标轴的交点、三角函数、三角形相似的性质和判定,并采用了分类讨论的思想解决第3个问题,本题若想求角的度数和三角函数值,需求出函数与两坐标轴的交点坐标,写出对应边的长度,从而解决问题.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:选择题
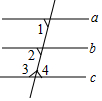 如图,下列推理错误的是( )
如图,下列推理错误的是( )| A. | ∵∠1=∠2,∴a∥b | B. | ∵b∥c,∴∠2=∠4 | ||
| C. | ∵a∥b,b∥c,∴a∥c | D. | ∵∠2+∠3=180°,∴a∥c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知菱形ABCD的对角线AC,BD相交于点O,延长AB至点E,使BE=AB,连接CE.
如图,已知菱形ABCD的对角线AC,BD相交于点O,延长AB至点E,使BE=AB,连接CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
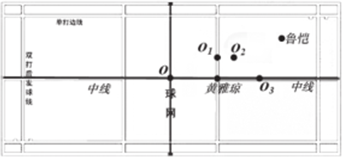 2017 全英羽毛球公开赛混双决赛,中国组合鲁恺/黄雅琼,对阵马来西亚里约奥运亚军陈炳顺/吴柳萤,鲁恺/黄雅琼两名小将的完美配合结果获胜.如图是羽毛球场地示意图,x 轴平行场地的中线,y 轴平行场地的球网线,设定鲁恺的坐标是(3,1),黄雅琼的坐标是(0,-1),则坐标原点为( )
2017 全英羽毛球公开赛混双决赛,中国组合鲁恺/黄雅琼,对阵马来西亚里约奥运亚军陈炳顺/吴柳萤,鲁恺/黄雅琼两名小将的完美配合结果获胜.如图是羽毛球场地示意图,x 轴平行场地的中线,y 轴平行场地的球网线,设定鲁恺的坐标是(3,1),黄雅琼的坐标是(0,-1),则坐标原点为( )| A. | O | B. | O1 | C. | O2 | D. | O3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
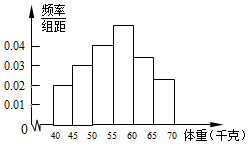 为了解全区5000名初中毕业生的体重情况,随机抽测了400名学生的体重,频率分布如图所示(每小组数据可含最小值,不含最大值),其中从左至右前四个小长方形的高依次为0.02、0.03、0.04、0.05,由此可估计全区初中毕业生的体重不小于60千克的学生人数约为1500人.
为了解全区5000名初中毕业生的体重情况,随机抽测了400名学生的体重,频率分布如图所示(每小组数据可含最小值,不含最大值),其中从左至右前四个小长方形的高依次为0.02、0.03、0.04、0.05,由此可估计全区初中毕业生的体重不小于60千克的学生人数约为1500人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com