
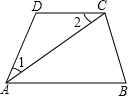
 如图,已知AC平分∠DAB,∠1=∠2.∠B=60°,求∠BCD的度数?
如图,已知AC平分∠DAB,∠1=∠2.∠B=60°,求∠BCD的度数?  赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
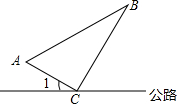 如图,在公路的同侧有A、B两个送奶站,C为公路上一个供奶站,CA和CB为供奶站路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边行走,速度为2.5km/h,问多长时间后这人距离B送奶站最近?
如图,在公路的同侧有A、B两个送奶站,C为公路上一个供奶站,CA和CB为供奶站路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边行走,速度为2.5km/h,问多长时间后这人距离B送奶站最近?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 正方形网格中,△ABC如图放置,则sin∠BAC=( )
正方形网格中,△ABC如图放置,则sin∠BAC=( )| A. | $\frac{2}{{\sqrt{13}}}$ | B. | $\frac{3}{{\sqrt{13}}}$ | C. | $\frac{4}{{\sqrt{13}}}$ | D. | $\frac{12}{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com