
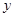 元,镜子的宽是
元,镜子的宽是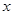 米.
米.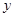 与
与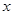 之间的关系式.
之间的关系式. 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 米.请利用下面所给的平面直角坐标系探索下列问题:
米.请利用下面所给的平面直角坐标系探索下列问题:
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
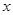 (月份)与市场售价
(月份)与市场售价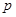 (元/千克)的关系如下表:
(元/千克)的关系如下表:上市时间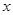 (月份) (月份) | 1 | 2 | 3 | 4 | 5 | 6 |
市场售价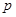 (元/千克) (元/千克) | 10.5 | 9 | 7.5 | 6 | 4.5 | 3 |
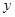 (元/千克)与上市时间
(元/千克)与上市时间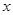 (月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).
(月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).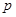 (元/千克)关于上市时间
(元/千克)关于上市时间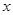 (月份)的函数关系式;
(月份)的函数关系式;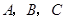 点,写出抛物线对应的函数关系式;
点,写出抛物线对应的函数关系式;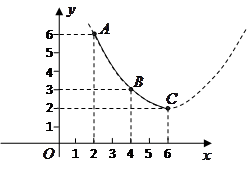
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
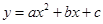 图象的一部分,图象过
图象的一部分,图象过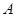 点(3,0),二次函数图象对称轴为
点(3,0),二次函数图象对称轴为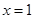 ,给出四个结论:①
,给出四个结论:①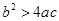 ;②
;②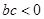 ;③
;③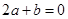 ;④
;④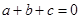 ,其中正确结论是( )
,其中正确结论是( )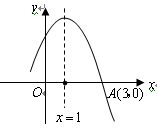
| A.②④ | B.①③ | C.②③ | D.①④ |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 厘米的细铁丝剪成两段.并把每段铁丝围成圆,设所得两圆半径分别为
厘米的细铁丝剪成两段.并把每段铁丝围成圆,设所得两圆半径分别为 和
和 .
.  与
与 的关系式,并写出
的关系式,并写出 的取值范围;
的取值范围; 的函数关系式,求S的最小值.
的函数关系式,求S的最小值.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
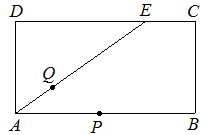
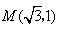 出发,沿射线OM方向以每秒1个单位长度的速度作匀速运动,在运动过程中,以OP为对角线的矩形OAPB的边长
出发,沿射线OM方向以每秒1个单位长度的速度作匀速运动,在运动过程中,以OP为对角线的矩形OAPB的边长 ;过点O且垂直于射线OM的直线
;过点O且垂直于射线OM的直线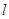 与点P同时出发,且与点P沿相同的方向、以相同的速度运动.
与点P同时出发,且与点P沿相同的方向、以相同的速度运动. 运动过程中,试判断AB与y轴的位置关系,并说明理由.
运动过程中,试判断AB与y轴的位置关系,并说明理由. 与直线L都运动了t秒,求此时的矩形OAPB与直线
与直线L都运动了t秒,求此时的矩形OAPB与直线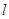 在运动过程中所扫过的区域的重叠部分的面积S(用含t的代数式表示).
在运动过程中所扫过的区域的重叠部分的面积S(用含t的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com