练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．在△ABC中，AB=8，AC=10，则BC边上的中线AD的取值范围是1＜AD＜9．

    分析 延长AD至E，使DE=AD，连接CE．根据SAS证明△ABD≌△ECD，得CE=AB，再根据三角形的三边关系即可求解．

    解答 解：延长AD至E，使DE=AD，连接CE．如图所示：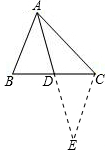
    在△ABD和△ECD中，$\left\{\begin{array}{l}{BD=CD}&{\;}\\{∠ADB=∠EDC}&{\;}\\{AD=ED}&{\;}\end{array}\right.$
    ∴△ABD≌△ECD（SAS），
    ∴CE=AB．
    在△ACE中，CE-AC＜AE＜CE+AC，
    即2＜2AD＜18，
    ∴1＜AD＜9．
    故答案为：1＜AD＜9．

    点评 此题综合运用了全等三角形的判定和性质、三角形的三边关系．注意：倍长中线是常见的辅助线之一．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．已知抛物线的表达式为y=-x2+6x+c．
    （1）若抛物线与x轴有交点，求c的取值范围；
    （2）设抛物线与x轴两个交点的横坐标分别为x1、x2，若x12+x22=26，求c的值；
    （3）若P、Q是抛物线上位于第一象限的不同两点，PA、QB都垂直于x轴，垂足分别为A、B，且△OPA与△OQB全等，求证：c＞-$\frac{21}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．在数轴上画出表示下列各数的点：2，-3，-1$\frac{1}{2}$，0，$\frac{3}{2}$，5，2$\frac{1}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

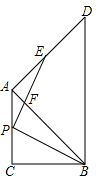    5．如图，已知△ABC和△ABD均为等腰直角三角形，∠ACB=∠BAD=90°，点P为边AC上任意一点（点P不与A、C两点重合），作PE⊥PB交AD于点E，交AB于点F．
    （1）求证：∠AEP=∠ABP．
    （2）猜想线段PB、PE的数量关系，并证明你的猜想．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．若m、n互为相反数，则|m-6+n|=6．若|-a|=5，则a=±5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．计算：
    （1）|-1|+18×（-$\frac{1}{3}$）2                   
    （2）4+（-12）×$\frac{1}{2}$-（-1）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知：A-B=7a2-7ab，且A=-4a2+6ab+7，
    （1）求B等于多少？
    （2）若|a+1|+（b-2）2=0，求B的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．m，n都是正数，多项式xm+xn+3xm+n的次数是（　　）
    A．2m+2nB．m或nC．m+nD．m，n中的较大数

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

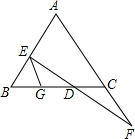    7．如图，已知，EG∥AF，请你从下面三个条件中，再选出两个作为已知条件，另一个作为结论，推出一个正确的命题．并证明这个命题（只写出一种情况）①AB=AC ②DE=DF ③BE=CF 
    已知：EG∥AF，AB=AC，DE=DF．
    求证：BE=CF．
    证明：
    作EG∥AF交BC于G，
    ∴∠EGB=∠ACB，∠GED=∠CFD，
    ∵AB=AC，
    ∴∠B=∠ACB，
    ∴∠B=∠EGB，
    ∴EB=EG，
    在△EGD和△FCD中，
    $\left\{\begin{array}{l}{∠GED=∠CFD}\\{DE=DF}\\{∠GDE=∠CDF}\end{array}\right.$，
    ∴EG=CF，
    ∴BE=CF．

    查看答案和解析>>

    同步练习册答案