
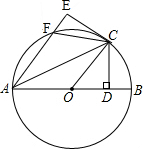
 如图,AB是⊙O的直径,C是⊙O上的一点,CD⊥AB于D.△ACD沿AC翻折后点D落在点E,AE交⊙O于点F;连接OC、FC.
如图,AB是⊙O的直径,C是⊙O上的一点,CD⊥AB于D.△ACD沿AC翻折后点D落在点E,AE交⊙O于点F;连接OC、FC.分析 (1)首先由翻折的性质,可得∠EAC=∠OAC,∠E=∠ADC=90°,然后判断出OC∥AE,即可推得∠OCE=90°,据此证得EC是⊙O的切线即可.
(2)首先根据OC∥AE,CF∥OA,判断出四边形AOCF是平行四边形;然后根据OA=OC,判断出四边形AOCF是菱形即可.
解答 (1)证明:如图1,
∵△ACD沿AC翻折后得到△ACF,
∴∠EAC=∠OAC,∠E=∠ADC=90°,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠EAC=∠OCA,
∴OC∥AE,
又∵∠E=90°,
∴∠OCE=90°,
∴CE⊥OC,
∵OC是⊙O的半径,
∴CE是⊙O的切线.
(2)证明:由(1),可得OC∥AE,
又∵CF∥OA,
∴四边形AOCF是平行四边形,
又∵OA=OC,
∴四边形AOCF是菱形.
点评 (1)此题主要考查了切线的性质和判定,切线必须满足两个条件:a、经过半径的外端;b、垂直于这条半径,否则就不是圆的切线.
(2)此题还考查了翻折变换(折叠问题),要熟练掌握,解答此题的关键是要明确:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
(3)此题还考查了菱形的性质和应用,要熟练掌握,解答此题的关键是要明确:①菱形具有平行四边形的一切性质;②菱形的四条边都相等; ③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;④菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:填空题
 如图,点E、F位于正方形ABCD边BC、CD上,且BE:EC=2:1,∠EAF=30°,则CF:FD=$\frac{1+13\sqrt{3}}{23}$.
如图,点E、F位于正方形ABCD边BC、CD上,且BE:EC=2:1,∠EAF=30°,则CF:FD=$\frac{1+13\sqrt{3}}{23}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
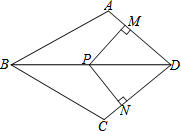 如图,在四边形ABCD中,DA=DC,P为对角线BD上一点,过点P作PM⊥AD,PN⊥CD,且PM=PN,
如图,在四边形ABCD中,DA=DC,P为对角线BD上一点,过点P作PM⊥AD,PN⊥CD,且PM=PN,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com