
【题目】如图,已知∠MON=30°,点 A1、A2、A3、…在射线 ON 上,点 B1、B2、B3、…在射线 OM 上;△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形.若 OA1=1,则△A2015B2015A2016 的边长为 ( )
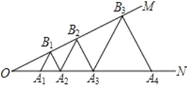
A. 4028 B. 4030 C. 22014 D. 22015
【答案】C
【解析】
试题∵△A1B1A2是等边三角形,∴A1B1=A2B1,∠3=∠4=∠12=60°,∴∠2=120°,∵∠MON=30°,∴∠1=180°﹣120°﹣30°=30°,又∵∠3=60°,∴∠5=180°﹣60°﹣30°=90°,∵∠MON=∠1=30°,∴OA1=A1B1=1,∴A2B1=1,∵△A2B2A3、△A3B3A4是等边三角形,∴∠11=∠10=60°,∠13=60°,∵∠4=∠12=60°,∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,∴∠1=∠6=∠7=30°,∠5=∠8=90°,∴A2B2=2B1A2,B3A3=2B2A3,∴A3B3=4B1A2=4,A4B4=8B1A2=8,A5B5=16B1A2=16,以此类推:△A2015B2015A2016的边长为 22014.故选C.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
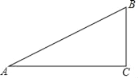
【题目】如图,Rt△ABC中,∠C=90°,∠A=30°.
(1)作线段AB的垂直平分线DE,垂足为点E,交AC于点D,要求用尺规作图,保留作图痕迹,标注有关字母,不要求写作法和证明;
(2)连接BD,直接写出∠CBD的度数;
(3)如果△BCD的面积为4,请求出△BAD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为 a 的正方形内去掉一个边长为 b 的小正方形(如图1),然后将剩余部分剪拼成一个矩形(如图2),上述操作所能验证的等式是( )
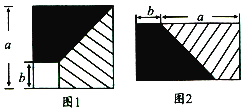
A. (a-b)2=a2-2ab+b2 B. a2+ab=a (a+b) C. (a+b)2=a2+2ab+b2 D. a2-b2=(a+b)(a-b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
(1)如图1,在圆内接正六边形ABCDEF中,半径OC=4,求正六边形的边长. 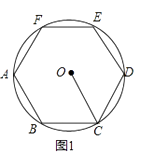
(2)如图2,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.求证:AB=AC. 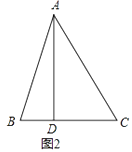
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从①∠1=∠2;②∠C=∠D;③∠A=∠F三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两直线AB,CD相交于点O,已知OE平分∠BOD,且∠AOC:∠AOD=3:7,

(1)求∠DOE的度数;
(2)若OF⊥OE,求∠COF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿∠CAB的角平分线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
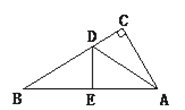
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平移三角形ABD,使点D沿BD的延长线平移至点C,得到三角形△A'B'D',A'B'交AC于点E,AD平分∠BAC.
(1)猜想∠B'EC与∠A'之间的关系,并写出理由;
(2)如果将三角形ABD平移至如图2所示位置,得到△A'B'D',请问:A'D'平分∠B'A'C吗?为什么?
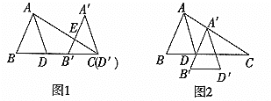
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com