
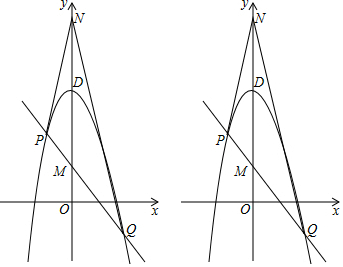
���� ��1�������ô���ϵ������������PQ�Ľ���ʽ���ڸ��ݶԳ������ֱ��PN�Ľ���ʽ������������ߵĽ���ʽ���ⷽ���������P���꼴�ɽ�����⣮
��2���ɣ�1����̽�����֣�DN=DM��
��3����PE��ON��E��QF��y����F���ɡ�NPE�ס�NQF���Ƴ�$\frac{NE}{PE}$=$\frac{NF}{QF}$���ɵ�$\frac{3-��k{x}_{P}+b��}{-{x}_{P}}$=$\frac{3-��k{x}_{Q}+b��}{{x}_{Q}}$��������3��xp+xQ��-2k��xP•xQ��-b��xP+xQ��=0��$\left\{\begin{array}{l}{y=-{x}^{2}+a}\\{y=kx+b}\end{array}\right.$����ȥy�õ���x2+kx+b-a=0���ɵ�xP+xQ=-k��xP•xQ=b-a���Ƴ�-3k-2k��b-a��+bk=0���Ƴ�b=2a-3���Ƴ�ֱ��PQ��y��Ľ���M������Ϊ��0��2a-3�����Ƴ�DM=3-a��DN=3-a���ɴ˼��ɽ�����⣮
��� �⣻��1������Q��2��-2������PΪ��$-\frac{1}{2}��\frac{7}{4}$��ʱ����ֱ��PQ�Ľ���ʽΪy=kx+b��
����$\left\{\begin{array}{l}{2k+b=-2}\\{-\frac{1}{2}k+b=\frac{7}{4}}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-\frac{3}{2}}\\{b=1}\end{array}\right.$��
��ֱ��PQ�Ľ���ʽΪy=-$\frac{3}{2}$x+1��
��Q��2��-3��ʱ�����ݶԳ��Կ�ֱ֪��NP�����㣨-2��-3����
��Q��2��-3������y=-x2+a�õ�a=1��
��ֱ��PN�Ľ���ʽΪy=3x+3��
��$\left\{\begin{array}{l}{y=3x+3}\\{y=-{x}^{2}+1}\end{array}\right.$�����$\left\{\begin{array}{l}{x=-2}\\{y=-3}\end{array}\right.$��$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$��
���P��������-1��0��
��ֱ��PQ�Ľ���ʽΪy=-x-1��
�ʴ𰸷ֱ�Ϊy=-$\frac{3}{2}$x+1����-1��0����y=-x-1��
��2���ɣ�1����֪����Q��2��-2������PΪ��$-\frac{1}{2}��\frac{7}{4}$��ʱ��DN=DM=1��
����Q��2��-3��ʱ��DN=DM=2��
���Բ���ND=MD��
��3����P�����꣨xp��yp����Q�����꣨xq��yq������PE��ON��E��QF��y����F��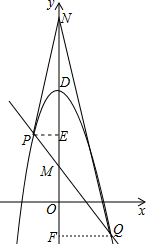
�ߡ�PNE=��QNF����PEN=��QFN=90�㣬
���NPE�ס�NQF��
��$\frac{NE}{PE}$=$\frac{NF}{QF}$��
��$\frac{3-��k{x}_{P}+b��}{-{x}_{P}}$=$\frac{3-��k{x}_{Q}+b��}{{x}_{Q}}$��
������3��xp+xQ��-2k��xP•xQ��-b��xP+xQ��=0
��$\left\{\begin{array}{l}{y=-{x}^{2}+a}\\{y=kx+b}\end{array}\right.$����ȥy�õ���x2+kx+b-a=0��
��xP+xQ=-k��xP•xQ=b-a��
��-3k-2k��b-a��+bk=0��
��b=2a-3��
��ֱ��PQ��y��Ľ���M������Ϊ��0��2a-3����
��DM=3-a��DN=3-a��
��DN=DM��
���� ���⿼����κ��������ʡ�һ�κ��������ʡ���ƽ���ߵĶ��塢���������ε��ж������ʡ�һԪ���η��̵ĸ���ϵ���Ĺ�ϵ��֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�ṹ��һ�κ��������÷����������꣬ѧ�����ò����������̣�������ת��Ϊ���̽���������п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x2 | B�� | 2x4 | C�� | 2x | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4��5��6 | B�� | 1.5��2��2.5 | C�� | 2��3��4 | D�� | 1��$\sqrt{2}$��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0��1֮�� | B�� | 1��2֮�� | C�� | 2��3֮�� | D�� | 3��4֮�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 0 | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x% | B�� | 1+2x% | C�� | ��1+x%��x% | D�� | ��2+x%��x% |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com