
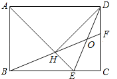
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①△ABE≌△AHD;②HE=CE;③H是BF的中点;④AB=HF;其中正确命题的个数为__________个.
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①△ABE≌△AHD;②HE=CE;③H是BF的中点;④AB=HF;其中正确命题的个数为__________个.
【答案】3
【解析】
根据题意,可知,ABE与AHD是等腰直角三角形,进而可得,AH=AB,AD=AE,根据三角形全等的判定方法,可证△ABE≌△AHD,①正确;根据矩形,等腰直角三角形和全等三角形的性质,可知,DH=AH=AB=BE,AD=AE=BC,进而,可得HE=CE,②正确;
根据等腰三角形的性质和三角形内角和定理,可得∠EBH=∠OHD=22.5°,进而可证明BEHHDF,即即H是BF的中点,③正确;由AB=AH,∠BAE=45°,可知,ABH不是等边三角形,进而可知,④错误.
∵在矩形ABCD中,∠BAD的平分线交BC于点E,DH⊥AE于点H,
∴∠BAE=∠HAD=45°,∠ABE=∠AHD=90°,
∴ABE与AHD是等腰直角三角形,
∴AD=![]() AH,AE=
AH,AE=![]() AB,
AB,
∵AD=![]() AB,
AB,
∴AH=AB,AD=AE,
在ABE与AHD中,
∵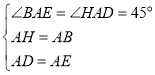
∴△ABE≌△AHD(SAS),故①正确;
∵在矩形ABCD中,ABE与AHD是等腰直角三角形,△ABE≌△AHD,
∴DH=AH=AB=BE,AD=AE=BC
∴AE-AH=BC-BE ,
∴HE=CE,故②正确;
∵AB=AH,
∴![]() ,
,
∴∠OHE=∠AHB=67.5°,
∴∠DHO=90°-67.5°=22.5°,
∵∠EBH=90°-67.5°=22.5°,
∴∠EBH=∠OHD,
在BEH和HDF中
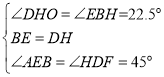
∴BEHHDF(ASA),
∴BH=HF,
即H是BF的中点,故③正确;
∵AB=AH,∠BAE=45°,
∴ABH不是等边三角形,
∴AB≠BH,
∴AB≠HF,故④错误,
综上所述,正确命题有3个,
故答案是:3


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
【题目】下列条件:①∠A=45°,AB=12,AC=15,∠A′=45°,A′B′=16,A′C′=20;②∠A=47°,AB=1.5,AC=2,∠B′=47°,A′B′=2.8,B′C′=2.1;③∠A=47°,AB=2,AC=3,∠B′=47°,A′B′=4,B′C′=6,其中能判定△ABC与△A′B′C′相似的有 ( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽和小华想利用摸球游戏决定谁去参加市里举办的书法比赛,游戏规则是:在一个不透明的袋子里装有除数字外完全相同的4个小球,上面分别标有数字2,3,4,5.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为偶数,则小丽去参赛;否则小华去参赛.
(1)用列表法或画树状图法,求小丽参赛的概率.
(2)你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师举了以下的例题:
例1等腰三角形ABC中,![]() ,求
,求![]() 的度数.(答案:35°)
的度数.(答案:35°)
例2等腰三角形ABC中,![]() ,求
,求![]() 的度数.(答案:40°或70°或100°)
的度数.(答案:40°或70°或100°)
张老师启发同学们编题,小刚编了如下一题:
(1)等腰三角形ABC中,![]() ,则
,则![]() 的度数为______;(2)小刚发现,
的度数为______;(2)小刚发现,![]() 的度数不同,得到
的度数不同,得到![]() 的度数的个数也可能不同.如果在等腰三角形ABC中,设
的度数的个数也可能不同.如果在等腰三角形ABC中,设![]() ,当
,当![]() 有三个不同的度数时,x的取值范围是______.
有三个不同的度数时,x的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
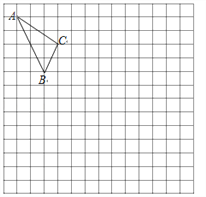
【题目】在如图的正方形网格中,每一个小正方形的边长为1.格点三角形![]() (顶点是网格线交点的三角形)的顶点
(顶点是网格线交点的三角形)的顶点![]() 的坐标分别是
的坐标分别是![]() .
.
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(3)请在![]() 轴上求作一点
轴上求作一点![]() ,使
,使![]() 的周长最小,并写出点
的周长最小,并写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店销售一批衬衫,每件进价![]() 元,开始以每件
元,开始以每件![]() 元的价格销售,每星期能卖出
元的价格销售,每星期能卖出![]() 件,后来因库存积压,决定降价销售,经两次降价后的每件售价
件,后来因库存积压,决定降价销售,经两次降价后的每件售价![]() 元,每星期能卖出
元,每星期能卖出![]() 件.
件.
![]() 已知两次降价百分率相同,求每次降价的百分率;
已知两次降价百分率相同,求每次降价的百分率;
![]() 聪明的店主在降价过程中发现,适当的降价既可增加销售又可增加收入,且每件衬衫售价每降低
聪明的店主在降价过程中发现,适当的降价既可增加销售又可增加收入,且每件衬衫售价每降低![]() 元,销售会增加
元,销售会增加![]() 件,若店主想要每星期获利
件,若店主想要每星期获利![]() 元,应把售价定为多少元?
元,应把售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
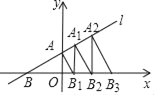
【题目】如图,在平面直角坐标系中,直线l:y=![]() x+1交x轴于点B,交y轴于点A,过点A作AB1⊥AB交x轴于点B1,过点B1作B1A1⊥x轴交直线l于点A2…依次作下去,则点Bn的横坐标为_____.
x+1交x轴于点B,交y轴于点A,过点A作AB1⊥AB交x轴于点B1,过点B1作B1A1⊥x轴交直线l于点A2…依次作下去,则点Bn的横坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
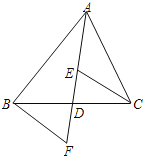
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE.下列说法:①△BDF≌△CDE;②CE=BF; ③BF∥CE;④△ABD和△ACD周长相等.其中正确的有___________(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() :
:![]() 与直线
与直线![]() :
:![]() 交于点
交于点![]() ,则
,则![]() ______.
______.

【答案】-1
【解析】
将点A的坐标代入两直线解析式得出关于m和b的方程组,解之可得.
解:由题意知![]() ,
,
解得![]() ,
,
故答案为:![]() .
.
【点睛】
本题主要考查两直线相交或平行问题,解题的关键是掌握两直线的交点坐标必定同时满足两个直线解析式.
【题型】填空题
【结束】
11
【题目】如图,长方形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则△AFC的面积等于___.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com