
【题目】如图,在平面直角坐标系内,⊙C与y轴相切于D点,与x轴相交于A(2,0)、B(8,0)两点,圆心C在第四象限.
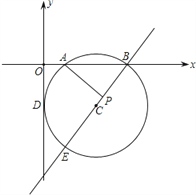
(1)求点C的坐标;
(2)连接BC并延长交⊙C于另一点E,若线段BE上有一点P,使得AB2=BPBE,能否推出AP⊥BE?请给出你的结论,并说明理由;
(3)在直线BE上是否存在点Q,使得AQ2=BQEQ?若存在,求出点Q的坐标;若不存在,也请说明理由.
【答案】(1)C(5,-4)(2)能,理由见解析(3)Q1(5, -4) Q2(5.84,-2.88)Q3(![]() ,
,![]() )
)
【解析】解: ⑴ C(5,-4);(过程1分,纵、横坐标答对各得1分) ………… 3分
⑵ 能 …………………………………4分
连结AE ,∵BE是⊙O的直径, ∴∠BAE=90°. …………5分
在△ABE与△PBA中,AB2=BP· BE , 即![]() , 又∠ABE=∠PBA,
, 又∠ABE=∠PBA,
∴△ABE∽△PBA . ……………………………………7分
∴∠BPA=∠BAE=90°, 即AP⊥BE . …………………8分
⑶ 分析:假设在直线EB上存在点Q,使AQ2=BQ· EQ. Q点位置有三种情况:
①若三条线段有两条等长,则三条均等长,于是容易知点C即点Q;
②若无两条等长,且点Q在线段EB上,由Rt△EBA中的射影定理知点Q即为AQ⊥EB之垂足;
③若无两条等长,且当点Q在线段EB外,由条件想到切割线定理,知QA切⊙C于点A.设Q(![]() ),并过点Q作QR⊥x轴于点R,由相似三角形性质、切割线定理、勾股定理、三角函数或直线解析式等可得多种解法.
),并过点Q作QR⊥x轴于点R,由相似三角形性质、切割线定理、勾股定理、三角函数或直线解析式等可得多种解法.
解题过程:
① 当点Q1与C重合时,AQ1=Q1B=Q1E, 显然有AQ12=BQ1· EQ1 ,
∴Q1(5, -4)符合题意; ……………………………9分
② 当Q2点在线段EB上, ∵△ABE中,∠BAE=90°
∴点Q2为AQ2在BE上的垂足, ……………………10分
∴AQ2=![]() = 4.8(或
= 4.8(或![]() ).
).
∴Q2点的横坐标是2+ AQ2·![]() ∠BAQ2= 2+3.84=5.84,
∠BAQ2= 2+3.84=5.84,
又由AQ2·![]() ∠BAQ2=2.88,
∠BAQ2=2.88,
∴点Q2(5.84,-2.88),![]() ………………………11分
………………………11分
③方法一:若符合题意的点Q3在线段EB外,
则可得点Q3为过点A的⊙C的切线与直线BE在第一象限的交点.
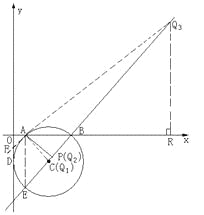
由Rt△Q3BR∽Rt△EBA,△EBA的三边长分别为6、8、10,
故不妨设BR=3t,RQ3=4t,BQ3=5t, ……………………12分
由Rt△ARQ3∽Rt△EAB得![]() , ………………………13分
, ………………………13分
即![]() 得t=
得t=![]() ,
,
〖注:此处也可由![]() 列得方程
列得方程![]() ; 或由AQ32= Q3B·Q3E=Q3R2+AR2列得方程
; 或由AQ32= Q3B·Q3E=Q3R2+AR2列得方程![]() )等等〗
)等等〗
∴Q3点的横坐标为8+3t=![]() , Q3点的纵坐标为
, Q3点的纵坐标为![]() ,
,
即Q3(![]() ,
,![]() ) . …………14分
) . …………14分
方法二:如上所设与添辅助线, 直线 BE过B(8, 0), C(5, -4),
∴直线BE的解析式是![]() . ………………12分
. ………………12分
设Q3(![]() ,
,![]() ),过点Q3作Q3R⊥x轴于点R,
),过点Q3作Q3R⊥x轴于点R,
∵易证∠Q3AR =∠AEB得 Rt△AQ3R∽Rt△EAB,
∴![]() , 即
, 即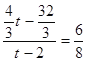 , ………………13分
, ………………13分
∴t=![]() ,进而点Q3的纵坐标为
,进而点Q3的纵坐标为![]() ,∴Q3(
,∴Q3(![]() ,
,![]() ). ………14分
). ………14分
方法三:若符合题意的点Q3在线段EB外,连结Q3A并延长交![]() 轴于F,
轴于F,
∴∠Q3AB =∠Q3EA,![]() ,
,
在R t△OAF中有OF=2×![]() =
=![]() ,点F的坐标为(0,
,点F的坐标为(0,![]() ),
),
∴可得直线AF的解析式为![]() , …………………12分
, …………………12分
又直线BE的解析式是![]() , ………………13分
, ………………13分
∴可得交点Q3(![]() ,
,![]() ). ……………………14分
). ……………………14分
(1)根据切割线定理求OD,,即可求得C的纵坐标,由图即可求得C的横坐标
(2)连结AE,通过AB2=BP· BE,求得△ABE∽△PBA, 因为BE是⊙O的直径, 所以∠BAE=90°,从而求得AP⊥BE
⑶假设在直线EB上存在点Q,使AQ2=BQ· EQ. Q点位置有三种情况:①若三条线段有两条等长,则三条均等长,于是容易知点C即点Q;②若无两条等长,且点Q在线段EB上,由Rt△EBA中的射影定理知点Q即为AQ⊥EB之垂足;③若无两条等长,且当点Q在线段EB外,由条件想到切割线定理,知QA切⊙C于点A.设Q(![]() ),并过点Q作QR⊥x轴于点R,由相似三角形性质、切割线定理、勾股定理、三角函数或直线解析式等可得多种解法.
),并过点Q作QR⊥x轴于点R,由相似三角形性质、切割线定理、勾股定理、三角函数或直线解析式等可得多种解法.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.同号两数相乘,取原来的符号
B.一个数与﹣1相乘,积为该数的相反数
C.一个数与0相乘仍得这个数
D.两个数相乘,积大于任何一个乘数
查看答案和解析>>
科目:初中数学 来源: 题型:
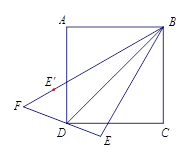
【题目】如图,四边形 ![]() 是正方形,
是正方形, ![]() 是
是 ![]() 垂直平分线上的点,点
垂直平分线上的点,点 ![]() 关于
关于 ![]() 的对称点是
的对称点是 ![]() ,直线
,直线 ![]() 与直线
与直线 ![]() 交于点
交于点 ![]() .
.
(1)若点 ![]() 是
是 ![]() 边的中点,连接
边的中点,连接 ![]() ,则
,则 ![]() =;
=;
(2)小明从老师那里了解到,只要点 ![]() 不在正方形的中心,则直线
不在正方形的中心,则直线 ![]() 与
与 ![]() 所夹锐角不变.他尝试改变点
所夹锐角不变.他尝试改变点 ![]() 的位置,计算相应角度,验证老师的说法.
的位置,计算相应角度,验证老师的说法.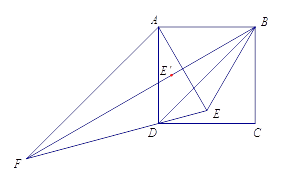
如图,将点 ![]() 选在正方形内,且△
选在正方形内,且△ ![]() 为等边三角形,求出直线
为等边三角形,求出直线 ![]() 与
与 ![]() 所夹锐角的度数;
所夹锐角的度数;
(3)请你继续研究这个问题,可以延续小明的想法,也可用其它方法.
我选择小明的想法;并简述求直线 ![]() 与
与 ![]() 所夹锐角度数的思路.
所夹锐角度数的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,动点A(a,0)在x轴的正半轴上,定点B(m, n)在第一象限内(m<2≤a).在△OAB外作正方形ABCD和正方形OBEF , 连接FD , 点M为线段FD的中点.作BB1⊥x轴于点B1 , 作FF1⊥x轴于点F1.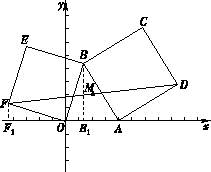
(1)填空:由△≌△ , 及B(m, n)可得点F的坐标为 , 同理可得点D的坐标为;(说明:点F , 点D的坐标用含m , n , a的式子表示)
(2)直接利用(1)的结论解决下列问题:
①当点A在x轴的正半轴上指定范围内运动时,点M总落在一个函数图象上,求该函数的解析式(不必写出自变量x的取值范围);
②当点A在x轴的正半轴上运动且满足2≤a≤8时,求点M所经过的路径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》卷九“勾股”中记载:今有户不知高广,竿不知长短.横之不出四尺,纵之不出二尺,斜之适出注.问户斜几何.
注释:横放,竿比门宽长出四尺;竖放,竿比门高长出二尺;斜放恰 好能出去.解决下列问题: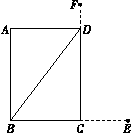
(1)示意图中,线段CE的长为尺,线段DF的长为尺;
(2)求户斜多长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘货船以每小时48海里的速度从港口B出发,沿正北方向航行.在港口B处时,测得灯塔A处在B处的北偏西37°方向上,航行至C处,测得A处在C处的北偏西53°方向上,且A、C之间的距离是45海里.在货船航行的过程中,求货船与灯塔A之间的最短距离及B、C之间的距离;若货船从港口B出发2小时后到达D,求A、D之间的距离.
(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
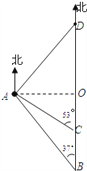
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a、b、c为平面上三条不同直线,
(1)若a∥b,b∥c,则a与c的位置关系是________;
(2)若a⊥b,b⊥c,则a与c的位置关系是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE;

(1)求证:△ACD≌△BCE;
(2)若∠D=50°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的偶数2,4,6,8…排列成如下的数表用十字框框出5个数(如图)
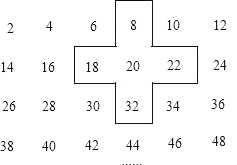
(1)十字框框出5个数的和与框子正中间的数20有什么关系?
(2)若将十字框上下左右平移,但一定要框住数列中的5个数,若设中间的数为a,用a的代数式表示十字框框住的5个数字之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com