
分析 (1)直接利用立方根的定义以及结合负指数幂的性质、零指数幂的性质、绝对值的性质分别化简得出答案;
(2)首先利用分式的混合运算法则化简分式,进而代入已知数据求出答案.
解答 解:(1)原式=3+$\sqrt{5}$-2-9+1
=$\sqrt{5}$-7;
(2)($\frac{{{a^2}-5a+2}}{a+2}$+1)÷$\frac{{{a^2}-4}}{{{a^2}+4a+4}}$,
=$\frac{{a}^{2}-5a+2+a+2}{a+2}$×$\frac{(a+2)^{2}}{(a+2)(a-2)}$
=$\frac{(a-2)^{2}}{a+2}$×$\frac{(a+2)^{2}}{(a+2)(a-2)}$
=a-2,
把a=2+$\sqrt{3}$代入得:
原式=2+$\sqrt{3}$-2=$\sqrt{3}$.
点评 此题主要考查了实数运算以及分式的混合运算,正确掌握相关运算法则是解题关键.


科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,6).
如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据求CD的长?(精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据求CD的长?(精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
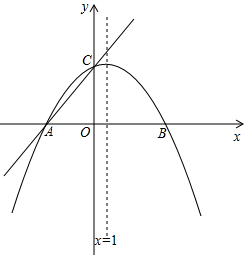 如图,在平面直角坐标系xOy中,一次函数y=$\frac{5}{4}$x+m(m为常数)的图象与x轴交于点A(-3,0),与y轴交于点C,以直线x=1为对称轴的抛物线y=ax2+bx+c(a、b、c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B
如图,在平面直角坐标系xOy中,一次函数y=$\frac{5}{4}$x+m(m为常数)的图象与x轴交于点A(-3,0),与y轴交于点C,以直线x=1为对称轴的抛物线y=ax2+bx+c(a、b、c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com