
【题目】在平行四边形ABCD中,∠A=45,BD⊥AD,BD=2
(1)求平行四边形ABCD的周长和面积
(2)求A、C两点间的距离

【答案】(1)![]() ;4(2)
;4(2)![]()
【解析】
(1)根据∠A=45,BD⊥AD可求得AD=BD=2,继而利用勾股定理可求得AB的长,然后再利用平行四边形的周长公式以及面积公式进行求解即可;
(2)联结AC,与BD相交于点O,在RtΔAOD 中,∠ADO=90°,根据勾股定理可求得OA的长,继而根据平行四边形对角的性质求得AC长即可.
(1)![]() BD⊥AD,
BD⊥AD,
![]() ∠ADB=90,
∠ADB=90,
又![]() ∠A=45,
∠A=45,
![]() ∠ABD=45 ,
∠ABD=45 ,
![]() AD=BD=2 ,
AD=BD=2 ,
![]() AB=
AB=![]() ,
,
![]() 四边形ABCD是平行四边形,
四边形ABCD是平行四边形,
![]() DC=AB=
DC=AB=![]() ,BC=AD=2,
,BC=AD=2,
![]()
![]() ,
,
![]()
![]() ;
;
(2)连结AC,与BD相交于点O,
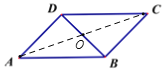
![]() 四边形ABCD是平行四边形,
四边形ABCD是平行四边形,
![]()
![]() ,
,![]() ,
,
![]() 在RtΔAOD中,∠ADO=90°,
在RtΔAOD中,∠ADO=90°,
![]()
![]() ,
,
![]()
![]() ,
,
所以A、C两点间的距离为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
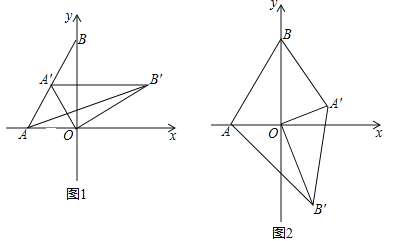
【题目】如图1,在平面直角坐标系,O为坐标原点,点A(﹣1,0),点B(0,![]() ).
).
(1)求∠BAO的度数;
(2)如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1,△BA′O的面积为S2,S1与S2有何关系?为什么?
(3)若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
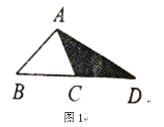
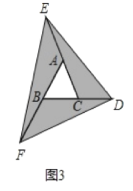
【题目】阅读理解,并完成填空:在图1至图3中,己知![]() 的面积为
的面积为![]() .
.
(1)如图1,延长![]() C的边
C的边![]() 到点
到点![]() ,使
,使![]() ,连结
,连结![]() .若
.若![]() 的面积为
的面积为![]() ,则
,则![]() __________(用含
__________(用含![]() 的代数式表示);
的代数式表示);
(2)如图2,延长![]() 的边
的边![]() 到点
到点![]() ,延长边
,延长边![]() 到点
到点![]() ,使
,使![]() ,
,![]() ,连结
,连结![]() ,若
,若![]() 的面积为
的面积为![]() ,则
,则![]() __________(用含
__________(用含![]() 的代数式表示);
的代数式表示);
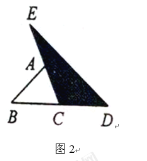
(3)在图2的基础上延长AB到点F,使BF=AB,连接FD,得到△DEF(如图3),若阴影部分的面积为S3,则S3=___(用含a的代数式表示)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第15次“移位”后,则他所处顶点的编号为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】声音在空气中传播的速度y(米/秒)是气温x (摄氏度)的一次函数,下表列出了一组不同气温时的音速.
气温x/摄氏度 | 0 | 5 | 10 | 15 | 20 |
音速y/(米/秒) | 331 | 334 | 337 | 340 | 343 |
(1)求y 与 x之间的函数关系式
(2)气温x=22(摄氏度)时,某人看到烟花燃放5秒后才听到声响,那么此人与燃放的烟花所在地相距多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两城间的铁路路程为1600千米,经过技术改造,列车实施了提速,提速后比提速前速度增加了20千米/小时,列车从甲城到乙城行驶时间减少4小时,这条铁路在现有条件下安全行驶速度不得超过140千米/小时,请你用学过的知识说明在这条铁路的现有条件下列车是否还可以再提速。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.

(1)如图1,连接AF、CE.求证:四边形AFCE为菱形.
(2)如图1,求AF的长.
(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.
①问在运动的过程中,以A、P、C、Q四点为顶点的四边形有可能是矩形吗?若有可能,请求出运动时间t和点Q的速度;若不可能,请说明理由.
②若点Q的速度为每秒0.8cm,当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
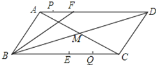
【题目】如图,![]() 中,点E是BC的中点,点F在AD上,AF=6cm,BF=12cm,BD平分∠FBC,若点P,Q分别是AF,BC上点,且CQ=2AP.若点P、Q、E、F为顶点的四边形构成平行四边形,则AP的长为______.
中,点E是BC的中点,点F在AD上,AF=6cm,BF=12cm,BD平分∠FBC,若点P,Q分别是AF,BC上点,且CQ=2AP.若点P、Q、E、F为顶点的四边形构成平行四边形,则AP的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆市的重大惠民工程--公租房建设已陆续竣工,计划10年内解决低收入人群的住房问题,前6年,每年竣工投入使用的公租房面积![]() 单位:百万平方米
单位:百万平方米![]() ,与时间x的关系是
,与时间x的关系是![]() 单位:年,
单位:年, ![]() 且x为整数
且x为整数![]() ;后4年,每年竣工投入使用的公租房面积
;后4年,每年竣工投入使用的公租房面积![]() 单位:百万平方米
单位:百万平方米![]() ,与时间x的关系是
,与时间x的关系是![]() 单位:年,
单位:年, ![]() 且x为整数
且x为整数![]() 假设每年的公租房全部出租完
假设每年的公租房全部出租完![]() 另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金
另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金![]() 单位:元
单位:元![]() 与时间
与时间![]() 单位:年,
单位:年, ![]() 且x为整数
且x为整数![]() 满足一次函数关系如下表:
满足一次函数关系如下表:
| 50 | 52 | 54 | 56 | 58 |
|
| 1 | 2 | 3 | 4 | 5 |
|
![]() 求出z与x的函数关系式;
求出z与x的函数关系式;
![]() 求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
![]() 若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高
若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高![]() ,这样可解决住房的人数将比第6年减少
,这样可解决住房的人数将比第6年减少![]() ,求a的值.
,求a的值.
![]() 参考数据:
参考数据: ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com