
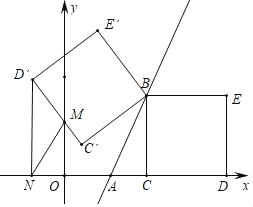
【题目】如图,在平面直角坐标系中,常数b<0,m>0,点A、B的坐标分别为(﹣![]() ,0)、(m,2m+b),正方形BCDE的顶点C、D分别在x轴的正半轴上.
,0)、(m,2m+b),正方形BCDE的顶点C、D分别在x轴的正半轴上.
(1)直接写出点D和点E的坐标(用含b、m的代数式表示);
(2)求![]() 的值;
的值;
(3)正方形BC′D′E′和正方形BCDE关于直线AB对称,点C′、D′、E′分别是点C、D、E的对称点,C′D′交y轴于点M,D′N⊥x轴,垂足为N,连接MN.
①若点N和点A关于y轴对称,求证:MN=MD′;
②若![]() ,求
,求![]() 的值.
的值.
【答案】(1)D(3m+b,0),E(3m+b,2m+b);(2)2;(3)①证明见解析;②1.
【解析】
(1)利用正方形性质得OA=-![]() ,OC=m,CD=DE=BE=BC=2m+b,OD=OC+CD=m+2m+b=3m+b;
,OC=m,CD=DE=BE=BC=2m+b,OD=OC+CD=m+2m+b=3m+b;
(2)由AC=OC﹣OA=m﹣(﹣![]() )得
)得
(3)①根据正方形和轴对称性质得∠ND'M=∠D'NM;
②由![]() ,变形
,变形![]() ,
,![]() ,最后得AD=3AO,由3m+
,最后得AD=3AO,由3m+![]() =3(
=3(![]() )
)
解得:b=﹣m即可.
解:(1)∵四边形BCDE是正方形
∴∠ACB=∠BCD=∠CDE=∠E=90°,BC=CD=DE=BE
∵A(﹣![]() ,0),B(m,2m+b),
,0),B(m,2m+b),
∴OA=-![]() ,OC=m,CD=DE=BE=BC=2m+b
,OC=m,CD=DE=BE=BC=2m+b
∴OD=OC+CD=m+2m+b=3m+b
∴D(3m+b,0),E(3m+b,2m+b)
(2)∵AC=OC﹣OA=m﹣(﹣![]() )=m+
)=m+![]()
∴
(3)①连接AC',
∵正方形BC′D′E′和正方形BCDE关于直线AB对称
∴AC'=AC,∠AC'B=∠ACB=90°
∵正方形BC'D'E'中,∠BC'D'=90°
∴∠AC'D'=90°+90°=180°,即点A、C'、D'在同一直线上
∵点N和点A关于y轴对称,M在y轴上
∴MN=MA
∴∠MNA=∠MAN
∵D'N⊥x轴
∴∠D'NA=∠D'NM+∠MNA=90°
∴∠ND'M+∠MAN=90°
∴∠ND'M=∠D'NM
∴MN=MD′

②∵![]()
∴![]()
∴![]()
∴![]()
∴AD2﹣AO2=8AO2
∴AD2=9AO2
∴AD=3AO
∵AD=OD﹣OA=3m+b﹣(![]() )=3m+
)=3m+![]()
∴3m+![]() =3(
=3(![]() )
)
解得:b=﹣m
∴![]() .
.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
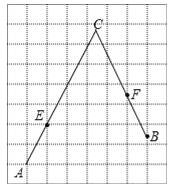
【题目】如图,在每个小正方形的边长为1的网格中,A,E为格点,B,F为小正方形边的中点,C为AE,BF的延长线的交点.
(Ⅰ)AE的长等于 ;
(Ⅱ)若点P在线段AC上,点Q在线段BC上,且满足AP=PQ=QB,请在如图所示的网格中,用无刻度的直尺,画出线段PQ,并简要说明点P,Q的位置是如何找到的(不要求证明) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两条射线BA//CD,PB和PC分别平分∠ABC和∠DCB,AD过点P,分别交AB,CD与点A,D.
(1)求∠BPC的度数;
(2)若![]() ,求AB+CD的值;
,求AB+CD的值;
(3)若![]() 为a,
为a,![]() 为b,
为b,![]() 为c,求证:a+b=c.
为c,求证:a+b=c.
查看答案和解析>>
科目:初中数学 来源: 题型:
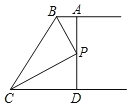
【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
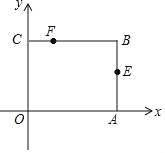
【题目】如图,矩形OABC放在以O为原点的平面直角坐标系中,A(3,0),C(0,2),点E是AB的中点,点F在BC边上,且CF=1,若M为x轴上的动点,N为y轴上的动点,则四边形MNFE的周长最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
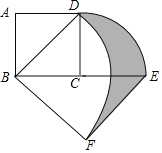
【题目】如图,正方形ABCD中,AB=2,将线段CD绕点C顺时针旋转90°得到线段CE,线段BD绕点B顺时针旋转90°得到线段BF,连接EF,则图中阴影部分的面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)求证:EG2=![]() GF
GF![]() AF;
AF;
(3)若AB=4,BC=5,求GF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市卫生局为了了解该市社区医院对患者随访情况,随机抽查了部分社区医院一年来对患者随访的次数,并用得到的数据绘制了两幅统计图,下面给出了两幅不完整的统计图:
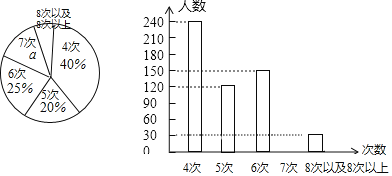
请根据图中提供的信息,回答下列问题:
(1)该市卫生局共抽查了社区医院的患者多少人?并补全条形统计图;
(2)请直接写出在这次抽样调查中的众数是 ,中位数是 ;
(3)如果该市社区医院患者有60000人,请你估计“随访的次数不少于7次”社区医院的患者有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,直径AB=8,∠A=30°,AC=8![]() ,AC与⊙O交于点D.
,AC与⊙O交于点D.
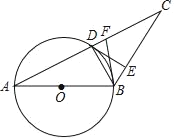
(1)求证:直线BD是线段AC的垂直平分线;
(2)若过点D作DE⊥BC,垂足为E,求证:DE是⊙O的切线;
(3)若点F是AC的三等分点,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com