
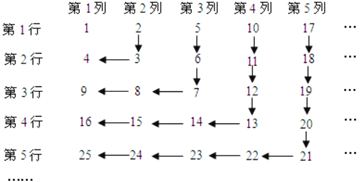
【题目】(题文)正整数按图中的规律排列,请写出第18行,第20列的数字:_____.
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
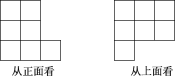
【题目】用小立方体搭成一个几何体,从正面和上面看到该几何体的形状图如图所示,搭建这样的几何体最多要几个小立方体?最少要几个小立方体?并画出最多和最少时从左面看到的形状图.
查看答案和解析>>
科目:初中数学 来源: 题型:
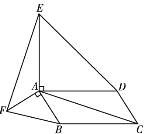
【题目】如图,在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE,∠FAB=∠EAD=90°,
连结AC、EF.在图中找一个与△FAE全等的三角形,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区准备新建50个停车位,用以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.6万元;新建3个地上停车位和2个地下停车位共需1.3万元.
(1)该小区新建1个地上停车位和1个地下停车位各需多少万元?
(2)该小区的物业部门预计投资金额超过12万元而不超过13万元,那么共有几种建造停车位的方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠C=90°,AC=8.BC=6,点P以每秒1个单位的速度从
A向C运动,同时点Q以每秒2个单位的速度从A→B→C方向运动,它们到C点后都
停止运动,设点P、Q运动的时间为t秒.
(Ⅰ)在运动过程中,请你用t表示P、Q两点间的距离,并求出P、Q两点间的距离
的最大值;
(Ⅱ)经过t秒的运动,求△ABC被直线PQ扫过的面积S与时间t的函数关系式.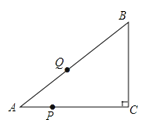
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R,S,若AQ=PQ,PR=PS,则这四个结论中正确的有( )
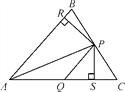
①PA平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP.
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,∠A=30°.分别以顶点A,B为圆心,大于![]() AB的长为半径作弧,两弧在直线AB两侧分别交于M,N两点,过M,N作直线交AB于点P,交AC于点D,连结BD.下列结论中,错误的是( )
AB的长为半径作弧,两弧在直线AB两侧分别交于M,N两点,过M,N作直线交AB于点P,交AC于点D,连结BD.下列结论中,错误的是( )
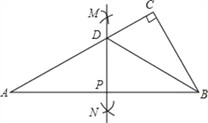
A. 直线AB是线段MN的垂直平分线 B. CD=![]() AD
AD
C. BD平分∠ABC D. S△APD=S△BCD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=90°,P是BC中点,∠EPF=90°,给出四个结论:①∠B=∠BAP;②AE=CF;③PE=PF;④S四边形AEPF=![]() S△ABC.其中成立的有_______
S△ABC.其中成立的有_______
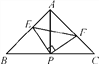
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角板的直角顶点O在直线AB上,OC,OD是三角板的两条直角边,OE平分∠AOD.
(1)若∠COE=20°,则∠BOD= ;若∠COE=α,则∠BOD= (用含α的代数式表示)
(2)当三角板绕O逆时针旋转到图2的位置时,其它条件不变,试猜测∠COE与∠BOD之间有怎样的数量关系?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com