
分析 (1)根据已知得出△≥0且a-6≠0,求出即可;
(2)根据根与系数的关系得出x1+x2=-$\frac{2a}{a-6}$,x1•x2=$\frac{a}{a-6}$,代入x1x2=4+x1+x2得求出即可.
解答 解:(1)∵一元二次方程(a-6)x2+2ax+a=0的两个实数根,
∴△=(2a)2-4(a-6)a≥0且a-6≠0,
解得:a≥0且a≠6;
(2)∵x1、x2是一元二次方程(a-6)x2+2ax+a=0的两个实数根,
∴由根与系数的关系得:x1+x2=-$\frac{2a}{a-6}$,x1•x2=$\frac{a}{a-6}$,
由-x1+x1x2=4+x2得:x1x2=4+x1+x2,
∴$\frac{a}{a-6}$=4-$\frac{2a}{a-6}$,
解得:a=24>且a≠6,
所以存在实数a,使-x1+x1x2=4+x2成立,此时a=24.
点评 本题考查了根的判别式和根与系数的关系,能根据根的判别式和根与系数的关系得出关于a的不等式和方程是解此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
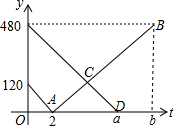 甲乙两城市之间有一条公路相连,公路中途穿过丙市,现有两位司机M、N相约各自同时从甲乙两地出发,途中M将一件物品交给N,已知M从甲市到丙市,N从乙市到甲市,N的速度是M的0.75,他们开车距离丙市的距离y(千米)与行驶的时间t(小时)的函数图象如图所示.
甲乙两城市之间有一条公路相连,公路中途穿过丙市,现有两位司机M、N相约各自同时从甲乙两地出发,途中M将一件物品交给N,已知M从甲市到丙市,N从乙市到甲市,N的速度是M的0.75,他们开车距离丙市的距离y(千米)与行驶的时间t(小时)的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
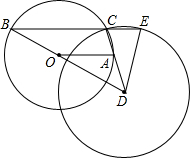 如图,在⊙O中,半径OA长为1,弦BC∥OA,射线BO,射线CA交于点D,以点D为圆心,CD为半径的⊙D交BC延长线于点E.
如图,在⊙O中,半径OA长为1,弦BC∥OA,射线BO,射线CA交于点D,以点D为圆心,CD为半径的⊙D交BC延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图①,AD为等腰直角△ABC的高,点A和点C分别在正方形DEFG的边DG和DE上,连接BG,AE.
如图①,AD为等腰直角△ABC的高,点A和点C分别在正方形DEFG的边DG和DE上,连接BG,AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
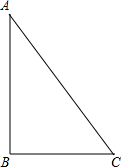 如图,在Rt△ABC中,∠ABC=90°,
如图,在Rt△ABC中,∠ABC=90°,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
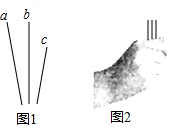 甲、乙、丙三人用三根完全相同的吸管玩游戏,将其中一根剪去一段(如图1所示),甲把三根吸管按如图2所示的方式拿在手中,使露出的部分完全相同,乙先从中抽取一根不放回,丙再从中抽取一根.
甲、乙、丙三人用三根完全相同的吸管玩游戏,将其中一根剪去一段(如图1所示),甲把三根吸管按如图2所示的方式拿在手中,使露出的部分完全相同,乙先从中抽取一根不放回,丙再从中抽取一根.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com