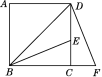
【题目】如图，BD为正方形ABCD的对角线，BE平分∠DBC，交DC于点E，延长BC到F，使CF＝CE，连接DF.若CE＝1 cm，则BF＝__________．
【答案】(2＋
) cm
【解析】
根据题意得CE=CF，则BF=BC+CF=CD+CE，而CD=DE+CE，关键是求出DE的长；由BE平分∠DBC，∠BCE=90°，可以作辅助线：过点E作EG⊥BD于点G，如图，利用角平分线的性质，得到GE=CE；接下来在等腰直角三角形DGE中，利用勾股定理求出DE的长，即可得出结论.
过点E作EG⊥BD于点G.
∵BE平分∠DBC，
∴GE=CE=1cm.
∵四边形ABCD为正方形，
∴∠GDE=45°.
又∵EG⊥BD，
∴∠EGD=90°，
∴∠GED=∠GDE=45°，
∴DG=GE=1cm.
根据勾股定理，得DE=cm，
∴BC=CD=(+1)cm.
又∵CE=CF，
∴BF=BC+CF=CD+CE=(+2)cm.
故答案为(+2)cm.
科目：初中数学 来源： 题型：
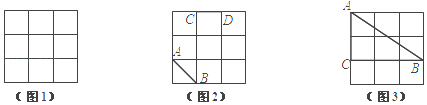
【题目】如图，正方形网格中的每个小正方形边长都是1．请同学们利用网格线进行画图：
(1)在图1中，画一个顶点为格点、面积为5的正方形；
(2)在图2中，已知线段AB、CD，画线段EF，使它与AB、CD组成轴对称图形；(要求画出所有符合题意的线段)
(3)在图3中，找一格点D，满足：①到CB、CA的距离相等；②到点A、C的距离相等．
查看答案和解析>>
科目：初中数学 来源： 题型：
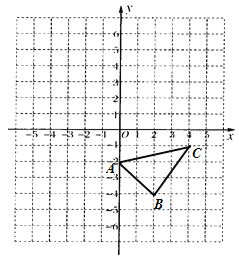
【题目】已知：如图，在平面直角坐标系中．
（1）作出△ABC关于
轴对称的
，并写出
三个顶点的坐标： 
（ ），
（ ），
（ ）；
（2）直接写出△ABC的面积为 ；
（3）在
轴上画点P，使PA+PC最小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某学校的复印任务原来由甲复印社承接，其收费y（元）与复印页数x（页）的关系如下表：
x（页） | 100 | 200 | 400 | 1000 | … |
y（元） | 40 | 80 | 160 | 400 |
（1）若y与x满足初中学过的某一函数关系，求函数的解析式;
（2）现在乙复印社表示：若学校先按每月付给200元的承包费，则可按每页0.15元收费，则乙复印社每月收费y（元）与复印页数x（页）的函数关系为________________，
（3）学校准备复印材料1000页，应选择哪个复印社比较优惠？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中
，AO=BO，直线MN经过点O, 且AC⊥MN于C，BD⊥MN于D
(1) 当直线MN绕点O旋转到图①的位置时，求证：CD=AC+BD；
(2) 当直线MN绕点O旋转到图②的位置时，求证：CD=AC-BD；
(3) 当直线MN绕点O旋转到图③的位置时，试问：CD、AC、BD有怎样的等量关系？请写出这个等量关系，并加以证明。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，点C在⊙O上，连接AC，BC，点D是BA延长线上一点，且AC=AD，若∠B=30°，AB=2，则CD的长是（ ）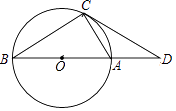
A.
B.2
C.1
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，∠ACB＝90°，D为AB的中点，四边形BCED为平行四边形，DE，AC相交于F.连接DC，AE.
（1）试确定四边形ADCE的形状，并说明理由．
（2）若AB＝16，AC＝12，求四边形ADCE的面积．
（3）当△ABC满足什么条件时，四边形ADCE为正方形？请给予证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，BD，CD分别是过⊙O上点B，C的切线，且∠BDC=120°，连接AC．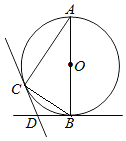 
（1）求∠A的度数；
（2）若点D到BC的距离为2，那么⊙O的半径是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
