
����Ŀ������y=x2+bx+c��ͼ����x �ύ��A��B���㣬��y�ύ�ڵ�C��OB=OC����D�ں���ͼ���ϣ�CD//x�ᣬ��CD=2��ֱ��l �������ߵĶԳ��ᣬE�������ߵĶ��㣮
��1����b��c ��ֵ��
��2����ͼ��������BE���߶�OC �ϵĵ�F ����ֱ��l �ĶԳƵ�F�� ǡ�����߶�BE�ϣ����F�����ꣻ
��3����ͼ��������P���߶�OB�ϣ�����P ��x ��Ĵ��߷ֱ���BC���ڵ�M���������߽��ڵ�N�����ʣ����������Ƿ���ڵ�Q��ʹ����PQN����APM�������ȣ����߶�NQ�ij�����С��������ڣ������Q�����ꣻ��������ڣ�˵�����ɣ�

ͼ �� ͼ��
���𰸡���1��c=-3����2����F������Ϊ��0��-2������3����������ĵ�Q������Ϊ��![]() ,
,![]() ����(
����(![]() ,
,![]() )
)
��������
��1������������������߶Գ�����������b��ֵ����OB=OC������c��ʾ��B�����������������߽���ʽ�����c��ֵ��
��2������F��0��m������ɱ�ʾ��F������������B��E����������ֱ��BE�Ľ���ʽ����F���������ֱ��BE����ʽ�ɵõ�����m�ķ����������F���������
��3�����P����Ϊ��n��0�����ɱ�ʾ��PA��PB��PN�ij�����QR��PN������ΪR��������QR�ij�����n�ɱ�ʾ��Q��R��N�����꣮��Rt��QRN�����ɹ��ɶ����ɵõ�����n�Ķ��κ��������ö��κ��������ʿ�֪��ȡ����Сֵʱn��ֵ��������Q���������
��1����CD��x����CD=2���������߶Գ���Ϊx=1����![]() ��
��
��OB=OC��C��0��c������B�������Ϊ����c��0������0=c2+2c+c�������c=��3��c=0����ȥ������c=��3��
��2�����F��������0��m����
�߶Գ���Ϊֱ��x=1�����F����ֱ��l�ĶԳƵ�F������Ϊ��2��m����
�ɣ�1����֪�����߽���ʽΪy=x2��2x��3=��x��1��2��4����E��1����4����
��ֱ��BE������B��3��0����E��1����4���������ô���ϵ�����ɵ�ֱ��BE�ı���ʽΪy=2x��6��
�ߵ�F��BE������m=2��2��6=��2������F������Ϊ��0����2����
��3�����ڵ�Q����������
���P������n��0������PA=n+1��PB=PM=3��n��PN=��n2+2n+3��
��QR��PN������ΪR��
��S��PQN=S��APM����![]() ����QR=1��
����QR=1��
������������ۣ�
�ٵ�Q��ֱ��PN�����ʱ��Q�������Ϊ��n��1��n2��4n����R�������Ϊ��n��n2��4n����N�������Ϊ��n��n2��2n��3��������Rt��QRN����NQ2=1+��2n��3��2����![]() ʱ��NQȡ��Сֵ1����ʱQ�������Ϊ
ʱ��NQȡ��Сֵ1����ʱQ�������Ϊ![]() ��
��
�ڵ�Q��ֱ��PN���Ҳ�ʱ��Q�������Ϊ��n+1��n2��4����
ͬ����NQ2=1+��2n��1��2����![]() ʱ��NQȡ��Сֵ1����ʱQ�������Ϊ
ʱ��NQȡ��Сֵ1����ʱQ�������Ϊ![]() ��
��
���Ͽ�֪������������ĵ�Q��������Ϊ![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˽�ҳ������ӣ���ͨҲԽ��Խӵ����ͨ������£�ij�ι�·�ϳ�������ʻ�ٶȣ�ǧ��/ʱ����·��ÿ����ӵ�г�������x�������Ĺ�ϵ��ͼ��ʾ����x��8ʱ��y��x�ɷ�����������ϵ�������ٶȵ���20ǧ��/ʱ����ͨ�ͻ�ӵ�£�Ϊ������ֽ�ͨӵ�£���·��ÿ����ӵ�г�������xӦ������ķ�Χ�ǣ�������

A. x��32 B. x��32 C. x��32 D. x��32
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ÿ��С�����εı߳�Ϊ1�ķ���ֽ�У��ѡ�ABC����ƽ��5������á�A1B1C1�����Ƶ�B1˳ʱ�뷽����ת90��á�A2B1C2.
��1������ƽ�ƺ���ת���ͼ�Σ���������Ӧ��ĸ.

��2������ӿ�ʼ��������������·���ij�.������ú��Це�ʽ�ӱ�ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
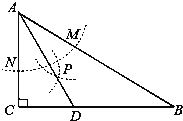
����Ŀ����ͼ������ABC�У���C=90������B=30������AΪԲ�ġ����ⳤΪ�뾶�����ֱ�AB��AC�ڵ�M��N���ٷֱ���M��NΪԲ�ģ�����![]() MN�ij�Ϊ�뾶�������������ڵ�P������AP���ӳ���BC�ڵ�D����������˵������DM=DN���ڡ�ADC=60�����۵�D��AB���д����ϣ���S��DAC:S��ABC=1:3��������ȷ�ĸ����ǣ� ��
MN�ij�Ϊ�뾶�������������ڵ�P������AP���ӳ���BC�ڵ�D����������˵������DM=DN���ڡ�ADC=60�����۵�D��AB���д����ϣ���S��DAC:S��ABC=1:3��������ȷ�ĸ����ǣ� ��
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ.
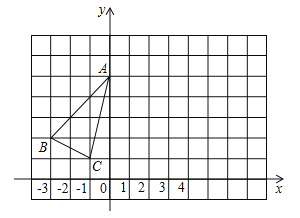
��1��������ABC����y��ԳƵ���AB1C1, ��д��B1�����ꣻ
��2������ABC����ƽ��8����λ, ����ƽ�ƺ����A2B2C2, д��B2�����ꣻ
��3������۲�������ͼ��, ��AB1C1����A2B2C2��������λ�ù�ϵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B���������ֱ�Ϊ��0��6������0��3������PΪx����������һ���㣬����A��AP�Ĵ��ߣ�����B��BP�Ĵ��ߣ������߽��ڵ�Q������PQ��MΪ�߶�PQ���е㣮

��1����֤��A��B��P��Q�ĵ�����MΪԲ�ĵ�ͬһ��Բ�ϣ�
��2������M��x������ʱ�����Q�����ꣻ
��3������P�ӵ㣨2��0���˶����㣨3��0��ʱ����ֱ��д���߶�QMɨ��ͼ�ε������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2����m+n+1��x+m��n��0��������ʵ����Ϊ�����£��Ҧ��ܦ£�
��1�����ú������µĴ���ʽ��ʾm��n��
��2����֤������1�ܦ£�
��3������P�������£�����ABC�����������˶�������ABC���������ֱ�ΪA��1��2����B��![]() ��1����C��1��1�������Ƿ���ڵ�P��ʹm+n=
��1����C��1��1�������Ƿ���ڵ�P��ʹm+n=![]() �������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڶԱ߲���ȵ��ı����У����ı��ε������Խ����ഹֱ����ô˳�������ı��θ����е�õ����ı�����( )
A.����B.����C.����D.������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com