
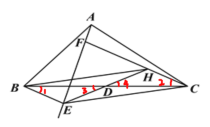
【题目】在△ABC中,D为BC中点,BE、CF与射线AE分别相交于点E、F(射线AE不经过点D).
(1)如图①,当BE∥CF时,连接ED并延长交CF于点H. 求证:四边形BECH是平行四边形;
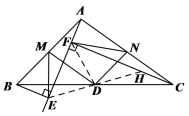
(2)如图②,当BE⊥AE于点E,CF⊥AE于点F时,分别取AB、AC的中点M、N,连接ME、MD、NF、ND. 求证:∠EMD=∠FND.


图① 图②
【答案】(1)见解析;(2)见解析
【解析】
(1)根据ASA证明△BDE≌△CDH.得ED=HD.又BD=CD,可得四边形BECH是平行四边形.
(2)连接FD、ED,延长ED交CF于点H,根据(1)可知ED=HD.可得ED=FD. 在Rt△AEB中,M是斜边AB中点,故![]() ,同理
,同理![]() .故ME=DN 同理,MD=NF. 由SSS证△MED≌△NDF.所以∠EMD=∠FND.
.故ME=DN 同理,MD=NF. 由SSS证△MED≌△NDF.所以∠EMD=∠FND.
证明:(1)∵D为BC中点,
∴BD=CD.
∵BE∥CF,
∴∠1=∠2.
又∵∠3=∠4,
∴△BDE≌△CDH.
∴ED=HD.
∴四边形BECH是平行四边形.
(2)连接FD、ED,延长ED交CF于点H,
∵BE⊥AE,CF⊥AE,
∴BE∥CF.
根据(1)可知ED=HD.
又∵CF⊥AE,
∴ED=FD.
∵Rt△AEB中,M是斜边AB中点,
∴![]() ,
,
∵△ABC中,D、N分别是BC、AC中点,
∴![]() .
.
∴ME=DN
同理,MD=NF.
∴△MED≌△NDF.
∴∠EMD=∠FND.


科目:初中数学 来源: 题型:
【题目】已知直线l上有一点O,点A,B同时从O出发,在直线l上分别向左,向右作匀速运动,且A,B的速度之比是1:2,设运动时间为ts,
(1)当t=2s时,AB=24cm,此时,
①在直线l上画出A,B两点运动2s时的位置,并回答点A运动的速度是 cm/s,点B的运动速度是 cm/s;
②若点P为直线l上一点,且PA=OP+PB,求![]() 的值;
的值;
(2)在(1)的条件下,若A,B同时按原速度向左运动,再经过几秒,OA=3OB?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC三个顶点的坐标分别为(1,2),(-2,3),(-1,0),把它们的横坐标和纵坐标都扩大到原来的2倍,得到点 ![]() ,
, ![]() ,
, ![]() .下列说法正确的是( )
.下列说法正确的是( ) 
A.△ ![]() 与△ABC是位似图形,位似中心是点(1,0)
与△ABC是位似图形,位似中心是点(1,0)
B.△ ![]() 与△ABC是位似图形,位似中心是点(0,0)
与△ABC是位似图形,位似中心是点(0,0)
C.△ ![]() 与△ABC是相似图形,但不是位似图形
与△ABC是相似图形,但不是位似图形
D.△ ![]() 与△ABC不是相似图形
与△ABC不是相似图形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆B位置的坐标;

(2)若体育馆位置坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2).
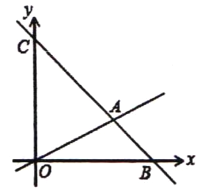
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)在y轴的负半轴上是否存在点M,使△ABM是以AB为直角边的直角角形?如果存在,求出点M的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
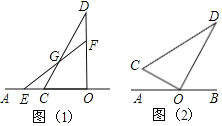
【题目】如图,已知点O在直线AB上,将一副直角三角板的直角顶点放在点O处,其中∠OCD=60°,∠OEF=45°.边OC、OE在直线AB上.
(1)如图(1),若CD和EF相交于点G,则∠DGF的度数是______°;
(2)将图(1)中的三角板OCD绕点O顺时针旋转30°至图(2)位置
①若将三角板OEF绕点O顺时针旋转180°,在此过程中,当∠COE=∠EOD=∠DOF时,求∠AOE的度数;
②若将三角板OEF绕点O以每秒4°的速度顺时针旋转180°,与此同时,将三角板OCD绕点O以每秒1°的速度顺时针旋转,当三角板OEF旋转到终点位置时,三角板OCD也停止旋转.设旋转时间为t秒,当OD⊥EF时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某产品的生产流水线每小时可生产100件产品,生产前没有产品积压,生产3h后安排工人装箱,若每小时装产品150件,未装箱的产品数量(y)是时间(x)的函数,那么这个函数的大致图像只能是( )
A. 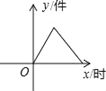 B.
B. 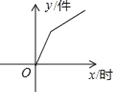 C.
C. 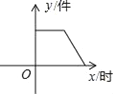 D.
D. 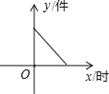
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com