
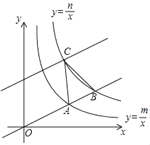
【题目】如图,直线y=![]() x分别与双曲线y=
x分别与双曲线y=![]() (m>0,x>0),双曲线y=
(m>0,x>0),双曲线y=![]() (n>0,x>0)交于点A和点B,且
(n>0,x>0)交于点A和点B,且![]() ,将直线y=
,将直线y=![]() x向左平移6个单位长度后,与双曲线y=
x向左平移6个单位长度后,与双曲线y=![]() 交于点C,若S△ABC=4,则
交于点C,若S△ABC=4,则![]() 的值为_____,mn的值为_____.
的值为_____,mn的值为_____.
【答案】![]() 100
100
【解析】
先求出直线y=![]() x向左平移6个单位长度后的解析式为y=
x向左平移6个单位长度后的解析式为y=![]() x+4,那么直线y=
x+4,那么直线y=![]() x+4交y轴于E(0,4),作EF⊥OB于F.根据互相垂直的两直线斜率之积为﹣1得出直线EF的解析式为y=﹣
x+4交y轴于E(0,4),作EF⊥OB于F.根据互相垂直的两直线斜率之积为﹣1得出直线EF的解析式为y=﹣![]() x+4,再求出F点的坐标,根据勾股定理求得EF,根据S△ABC=4,求出AB,那么根据
x+4,再求出F点的坐标,根据勾股定理求得EF,根据S△ABC=4,求出AB,那么根据![]()
![]() ,求得OA,进而求出A、B两点坐标,求出m、n即可解决问题.
,求得OA,进而求出A、B两点坐标,求出m、n即可解决问题.
解:直线y=![]() x向左平移6个单位长度后的解析式为y=
x向左平移6个单位长度后的解析式为y=![]() (x+6),即y=
(x+6),即y=![]() x+4,
x+4,
∴直线y=![]() x+4交y轴于E(0,4),作EF⊥OB于F.
x+4交y轴于E(0,4),作EF⊥OB于F.
可得直线EF的解析式为y=﹣![]() x+4,
x+4,
由 ,解得
,解得 ,即
,即![]() .
.
∴EF ,
,
∵S△ABC=4,
∴![]() ABEF=4,
ABEF=4,
∴AB![]() ,
,
∵![]() ,
,
∴OA=![]() AB=
AB=![]() ,
,
∴A(3,2),B(5,![]() ),
),
∴m=6,n=![]() ,
,
∴![]() ,mn=100.
,mn=100.

故答案是:![]() ,100.
,100.


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】△ABC中,BC=12,高AD=8,矩形EFGH的一边GH在BC上,顶点E、F分别在AB、AC上,AD与EF交于点M.
(1)求证:![]() ;
;
(2)设EF=x,EH=y,写出y与x之间的函数表达式;
(3)设矩形EFGH的面积为S,求S与x之间的函数表达式,并写出S的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在长方形ABCD中,AB=12cm,BC=10cm,点P从A出发,沿A→B→C→D的路线运动,到D停止;点Q从D点出发,沿D→C→B→A路线运动,到A点停止.若P、Q两点同时出发,速度分别为每秒lcm、2cm,a秒时P、Q两点同时改变速度,分别变为每秒2cm、![]() cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
(1)求出a值;
(2)设点P已行的路程为y1(cm),点Q还剩的路程为y2(cm),请分别求出改变速度后,y1、y2和运动时间x(秒)的关系式;
(3)求P、Q两点都在BC边上,x为何值时P、Q两点相距3cm?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备购买A、B两种零件,已知A种零件的单价比B种零件的单价多30元,而用900元购买A种零件的数量和用600元购买B种零件的数量相等.
(1)求A、B两种零件的单价;
(2)根据需要,工厂准备购买A、B两种零件共200件,工厂购买两种零件的总费用不超过14700元,求工厂最多购买A种零件多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某风景区内一座塔AB的高度,小明分别在塔的对面一楼房CD的楼底C、楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度.(sin30°=0.50,cos30°≈0.87,tan30°≈0.58)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达![]() 处时,测得小岛
处时,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛
方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向.如果航母继续航行至小岛
方向.如果航母继续航行至小岛![]() 的正南方向的
的正南方向的![]() 处,求还需航行的距离
处,求还需航行的距离![]() 的长.
的长.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:
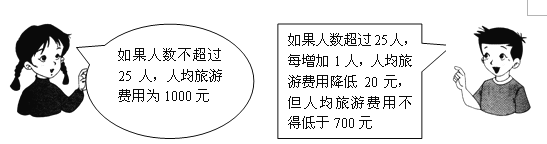 某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
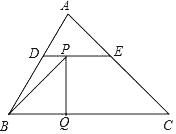
【题目】如图,在△ABC中,∠ABC=60°,∠C=45°,点D,E分别为边AB,AC上的点,且DE∥BC,BD=DE=2,CE=![]() ,BC=
,BC=![]() .动点P从点B出发,以每秒1个单位长度的速度沿B→D→E→C匀速运动,运动到点C时停止.过点P作PQ⊥BC于点Q,设△BPQ的面积为S,点P的运动时间为t,则S关于t的函数图象大致为( )
.动点P从点B出发,以每秒1个单位长度的速度沿B→D→E→C匀速运动,运动到点C时停止.过点P作PQ⊥BC于点Q,设△BPQ的面积为S,点P的运动时间为t,则S关于t的函数图象大致为( )
A. 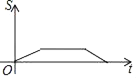 B.
B. 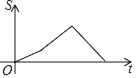
C. 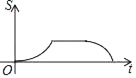 D.
D. 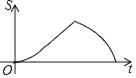
查看答案和解析>>
科目:初中数学 来源: 题型:
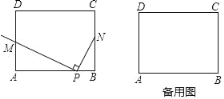
【题目】如图,在矩形ABCD中,AB=4,AD=3,点N为BC边上的一点,且BN=n(n>0),动点P从点A出发,以每秒1个单位长的速度沿AB边向点B运动,连接NP,作射线PM⊥NP交AD于点M,设点P运动的时间是t秒(t>0).
(1)当点M与点A重合时,t等于多少秒,当点M与点D重合时,n等于多少(用含字母t的代数式表示)
(2)若n=2,则
①在点P运动过程中,点M是否可以到达线段AD的延长线上?通过计算说明理由;
②连接ND,当t为何值时,ND∥PM?
(3)过点N作NK∥AB,交AD于点K,若在点P运动过程中,点K与点M不会重合,直接写出n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com