
【题目】解以下三个方程,并根据这三个方程的解的个数,讨论关于x的方程ax=b(其中a、b为常数)解的数量与a、b的取值的关系.
(1)2x+1=x+3
(2)3x+1=3(x﹣1)
(3)![]()
【答案】(1)x=2;(2)无解;(3)任意数;结论:当a≠0时,解是![]() ;当a=0时①当b=0时,任意数均为方程的解;②当b≠0时,方程无解.
;当a=0时①当b=0时,任意数均为方程的解;②当b≠0时,方程无解.
【解析】
将方程去分母,然后去括号,移项,合并同类项,系数化为1,即可求解.
解:(1)2x+1=x+3
2x﹣x=3﹣1
x=2
显然,x=2是方程2x+1=x+3的唯一解.
(2)3x+1=3(x﹣1)
3x﹣3x=﹣3﹣1
0x=﹣4
显然,无论x取何值,均不能使等式成立,所以方程3x+1=3(x﹣1)无解.
(3)![]()
![]()
0x=0
显然,无论x取何值,均可使方程成立,所以该方程的解为任意数.
由(1)(2)可归纳:关于x的方程ax=b(其中a、b为常数) 解的情况分以下几种:
当a≠0时,方程ax=b的解是![]() ;
;
当a=0时,又分两种情况:
①当b=0时,方程有无数个解,任意数均为方程的解;
②当b≠0时,方程无解.


科目:初中数学 来源: 题型:
【题目】下列说法:①![]() 的5倍与
的5倍与![]() 的和的一半用代数式表示是
的和的一半用代数式表示是![]() ;②
;②![]() ,
,![]() 都是单项式,也都是整式;③
都是单项式,也都是整式;③![]() (
(![]() 、
、![]() 、
、![]() 是常数,
是常数,![]() )是二次三项式;④
)是二次三项式;④![]() ,
,![]() ,5是
,5是![]() 的项;⑤单项式
的项;⑤单项式![]() 的系数是-1,次数是3,其中正确的个数是( )
的系数是-1,次数是3,其中正确的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工艺商场按标价销售某种工艺品时,每件可获利45元;按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.
(1)该工艺品每件的进价、标价分别是多少元?
(2)若每件工艺品按(1)中求得的进价进货,标价售出,工艺商场每天可售出该工艺品100件.若每件工艺品降价1元,则每天可多售出该工艺品4件.问每件工艺品降价多少元出售,每天获得的利润最大?获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
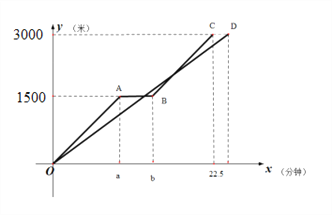
【题目】小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分)的关系如图所示,请结合图像,解答下列问题:
(1)a= b= ,m=
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AC⊥BC于C,BC=a,CA=b,AB=c,下列图形中⊙O与△ABC的某两条边或三边所在的直线相切,则⊙O的半径为![]() 的是( )
的是( )
A. 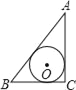 B.
B. 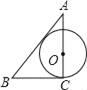 C.
C. 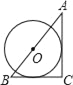 D.
D. 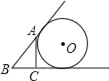
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在长方形和环形地块中铺设草坪,长方形的长、宽分别为a m、b m,环形的外圆、内圆的半径分别为R m、r m.
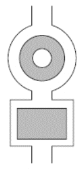
(1)求共需草皮的面积.
(2)若草皮每平方米需30元,当![]() 时,求草皮的费用.(保留π)
时,求草皮的费用.(保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=6,E是BC边的中点,点P在线段AD上,过P作PF⊥AE于F,设PA=x.
(1)求证:△PFA∽△ABE;
(2)当点P在线段AD上运动时,设PA=x,是否存在实数x,使得以点P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,请说明理由;
(3)探究:当以D为圆心,DP为半径的⊙D与线段AE只有一个公共点时,请直接写出x满足的条件: .

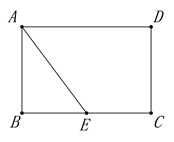
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,边长为2的正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一个动点(与点
上的一个动点(与点![]() 、
、![]() 不重合),过点
不重合),过点![]() 作
作![]() ,
,![]() 交射线
交射线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .
.
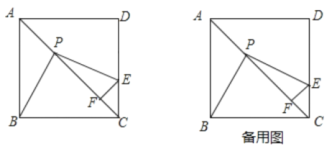
(1)求证:![]() :
:
(2)在点![]() 的运动过程中,
的运动过程中,![]() 的长度是否发生变化?若不变,试求出这个不变的值,写出解答过程:若变化,试说明理由:
的长度是否发生变化?若不变,试求出这个不变的值,写出解答过程:若变化,试说明理由:
(3)在点![]() 的运动过程中,
的运动过程中,![]() 能否为等腰三角形?如果能,直接写出此时
能否为等腰三角形?如果能,直接写出此时![]() 的长;如果不能,试说明理由.
的长;如果不能,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com