
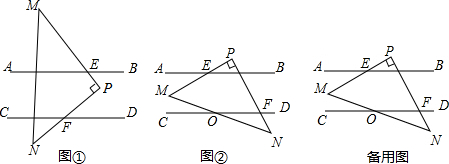
分析 (1)作PH∥AB,又AB∥CD,根据平行线的性质、对顶角相等解答;
(2)根据平行线的性质、三角形的外角的性质计算;
(3)利用(2)的结论、三角形内角和定理计算即可.
解答 解:(1)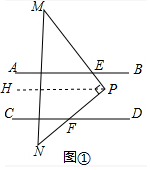 作PH∥AB,又AB∥CD,
作PH∥AB,又AB∥CD,
则PH∥CD,
∴∠PFD=∠MPH,∠AEM=∠HPM,
∵∠MPN=90°,
∴∠PFD+∠AEM=90°;
(2)∵AB∥CD,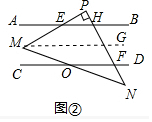 ∴∠PFD=∠PHB,
∴∠PFD=∠PHB,
∵∠PHB-∠PEB=90°,∠PEB=∠AEM,
∴∠PFD-∠AEM=90°;
(3)由(2)得,∠PFD=90°+∠PEH=120°,
∴∠N=180°-∠DON-∠PFD=45°.
点评 本题考查的是三角形内角和定理的应用、三角形的外角的性质、平行线的性质,掌握三角形内角和定理、正确作出辅助性是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
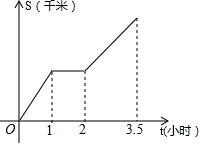 星期天,小明从家出发,以15千米/小时的速度骑车去郊游,到达目的地休息一段时间后原路返回,已知小明行驶的路程s(千米)与时间t(小时)之间的函数关系如图所示,则小明返程的速度为( )
星期天,小明从家出发,以15千米/小时的速度骑车去郊游,到达目的地休息一段时间后原路返回,已知小明行驶的路程s(千米)与时间t(小时)之间的函数关系如图所示,则小明返程的速度为( )| A. | 15千米/小时 | B. | 10千米/小时 | C. | 6千米/小时 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com