
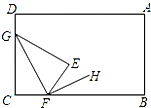
 如图所示,将一张长方形纸片AB-CD的∠C沿CF折叠(F在BC边上,不与B,C重合),使得C点落在长方形ABCD内部E处,FH平分∠BFE,则∠GFH的度数满足( )
如图所示,将一张长方形纸片AB-CD的∠C沿CF折叠(F在BC边上,不与B,C重合),使得C点落在长方形ABCD内部E处,FH平分∠BFE,则∠GFH的度数满足( )| A. | ∠GFH<90° | B. | ∠GFH=90° | C. | ∠GFH>90° | D. | 0°<∠GFH<90° |
分析 因为折叠后两个三角形全等,所以∠CFG=∠GFE,因为FH是∠BFE的平分线,所以∠EFH=∠HFB.由于∠GFH=∠GFE+EFH,可通过平角关系求出∠GFH的度数.
解答 解:∵△CFG折叠成△EFG,∴△CFG≌△EFG,∴∠CFG=∠GFE=$\frac{1}{2}$∠GCE;
∵FH是∠BFE的平分线,所以∠EFH=∠HFB=$\frac{1}{2}$∠BFE.
∵∠GCE+∠BFE=180°,
∴∠GFH=∠GFE+EFH=$\frac{1}{2}$∠GCE+$\frac{1}{2}$∠BFE=$\frac{1}{2}$(∠GCE+∠BFE)=90°.
故选B.
点评 本题考查了折叠后两个图形间的关系和、角的平分线及角的和差关系.解决本题利用了邻补角互补的性质.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC中,∠ACB=90°,在BC上截取CD=AC,E在AB上,∠CED=90°,CE=2,ED=1,F是AB的中点,点G在CB上,∠GFB=2∠ECB,则GF的长为$\frac{\sqrt{5}}{2}$.
如图,△ABC中,∠ACB=90°,在BC上截取CD=AC,E在AB上,∠CED=90°,CE=2,ED=1,F是AB的中点,点G在CB上,∠GFB=2∠ECB,则GF的长为$\frac{\sqrt{5}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,边长为8的等边△ABC,AD⊥BC于D,点E是线段AD上的一个动点,CF=CE,∠ECF=60°,则线段DF长的取值范围是4≤DF≤4$\sqrt{7}$.
如图,边长为8的等边△ABC,AD⊥BC于D,点E是线段AD上的一个动点,CF=CE,∠ECF=60°,则线段DF长的取值范围是4≤DF≤4$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知Rt△ABC中,∠ABC=90°,BC=9,cosC=$\frac{3}{5}$,D是边AC上的动点,连接BD,过点D作ED⊥BD,交射线BA于点E,当△AED是等腰三角形时,CD的值为3或$\frac{54}{5}$.
如图,已知Rt△ABC中,∠ABC=90°,BC=9,cosC=$\frac{3}{5}$,D是边AC上的动点,连接BD,过点D作ED⊥BD,交射线BA于点E,当△AED是等腰三角形时,CD的值为3或$\frac{54}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com