
 某数学兴趣小组为了估计河的宽度,在河对岸选定一个8标点P,在近岸取点Q和S,使点P,Q,S共线且直找PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QS=60m,请计算河的宽度PQ.
某数学兴趣小组为了估计河的宽度,在河对岸选定一个8标点P,在近岸取点Q和S,使点P,Q,S共线且直找PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QS=60m,请计算河的宽度PQ. 分析 先证明△PQR∽△PSR,利用相似比得到$\frac{PQ}{PQ+QS}$=$\frac{QR}{ST}$,然后根据比例的性质求PQ.
解答 解:∵RQ⊥PS,TS⊥PS,
∴RQ∥TS,
∴△PQR∽△PSR,
∴$\frac{PQ}{PS}$=$\frac{QR}{ST}$,
∴$\frac{PQ}{PQ+QS}$=$\frac{QR}{ST}$,
∵QR=45m,ST=90m,QS=60m,
∴$\frac{PQ}{PQ+45}$=$\frac{60}{90}$,
∴PQ=90(m).
答:河的宽度PQ是90m.
点评 本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度(测量距离);借助标杆或直尺测量物体的高度.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
 如图,AC与BD交于O点,AB∥DC,AB=DC.
如图,AC与BD交于O点,AB∥DC,AB=DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
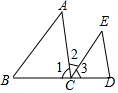 如图,点C在BD上,请分别根据已知条件进行推理,并在括号内注明推理根据.
如图,点C在BD上,请分别根据已知条件进行推理,并在括号内注明推理根据.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com