|
|
|
如图,在□ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.
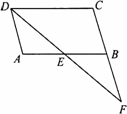
(1)求证:△ADE≌△BFE.
(2)若DF平分∠ADC,连接CE.试判断CE和DF的位置关系,并说明理由.
|
|
|
答案:
解析:
|
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADE=∠F.
∵点E是AB边的中点,
∴AE=BE.
在△ADE与△BFE中,
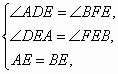
∴△ADE≌△BFE.
(2)解:CE⊥DF.理由如下:
连接CE.
由(1)知,△ADE≌△BFE,
∴DE=FE,即点E是DF的中点.
∵DF平分∠ADC,
∴∠ADE=∠CDE.
又由(1)知,∠ADE=∠BFE,∴∠CDE=∠BFE,
∴CD=CF.
又E为DF的中点,
∴CE⊥DF.
|
练习册系列答案
相关习题
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
下列说法正确的是
①平行四边形的两组对边分别相等;
②平行四边形的对角线相等;
③夹在平行线间的平行线段相等.
|
| [ ] |
A. |
①②
|
B. |
①②③
|
C. |
①③
|
D. |
②
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
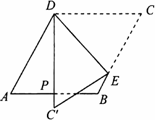
如图,在菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE,则∠DEC的大小为
|
| [ ] |
A. |
78°
|
B. |
75°
|
C. |
60°
|
D. |
45°
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
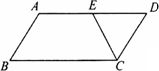
如图,在□ABCD中,AD=2AB,CE平分∠BCD交AD边于点E,且AE=3,则AB的长为
|
| [ ] |
A. |
4
|
B. |
3
|
C. |
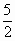
|
D. |
2
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
如图,在△ABC中,∠ABC=90°,BD为AC边上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,CF=6,则四边形BDFG的周长为________.
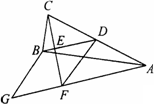
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
下列二次根式中,是最简二次根式的为
|
| [ ] |
A. |
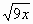
|
B. |
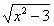
|
C. |
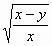
|
D. |
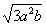
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:
①AB∥CD,AD∥BC;
②AB=CD,AD=BC;
③AO=CO,BO=DO;
④AB∥CD,AD=BC.
其中一定能判断四边形ABCD是平行四边形的条件共有
|
| [ ] |
A. |
1组
|
B. |
2组
|
C. |
3组
|
D. |
4组
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
下列二次根式中,属于最简二次根式的是
|
| [ ] |
A. |
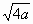
|
B. |
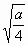
|
C. |
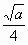
|
D. |
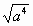
|
|
|
查看答案和解析>>
