
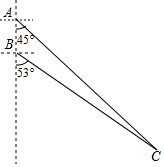
 如图所示,我国两艘海监船A,B在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船C,此时,B船在A船的正南方向5海里处,A船测得渔船C在其南偏东45°方向,B船测得渔船C在其南偏东53°方向,已知A船的航速为30海里/小时,B船的航速为25海里/小时,问C船至少要等待多长时间才能得到救援?(参考数据:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$,$\sqrt{2}$≈1.41)
如图所示,我国两艘海监船A,B在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船C,此时,B船在A船的正南方向5海里处,A船测得渔船C在其南偏东45°方向,B船测得渔船C在其南偏东53°方向,已知A船的航速为30海里/小时,B船的航速为25海里/小时,问C船至少要等待多长时间才能得到救援?(参考数据:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$,$\sqrt{2}$≈1.41) 分析 如图作CE⊥AB于E.设AE=EC=x,则BE=x-5,在Rt△BCE中,根据tan53°=$\frac{EC}{BE}$,可得$\frac{4}{3}$=$\frac{x}{x-5}$,求出x,再求出BC、AC,分别求出A、B两船到C的时间,即可解决问题.
解答 解:如图作CE⊥AB于E.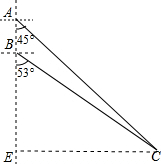
在Rt△ACE中,∵∠A=45°,
∴AE=EC,设AE=EC=x,则BE=x-5,
在Rt△BCE中,
∵tan53°=$\frac{EC}{BE}$,
∴$\frac{4}{3}$=$\frac{x}{x-5}$,
解得x=20,
∴AE=EC=20,
∴AC=20$\sqrt{2}$=28.2,
BC=$\frac{EC}{sin53°}$=25,
∴A船到C的时间≈$\frac{28.2}{30}$=0.94小时,B船到C的时间=$\frac{25}{25}$=1小时,
∴C船至少要等待0.94小时才能得到救援.
点评 本题考查解直角三角形的应用-方向角问题、锐角三角函数、速度、时间、路程之间的关系等知识,解题的关键是学会构建方程解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
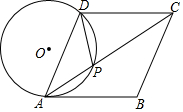 如图,在菱形ABCD中,点P在对角线AC上,且PA=PD,⊙O是△PAD的外接圆.
如图,在菱形ABCD中,点P在对角线AC上,且PA=PD,⊙O是△PAD的外接圆.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 95分,95分 | B. | 95分,90分 | C. | 90分,95分 | D. | 95分,85分 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
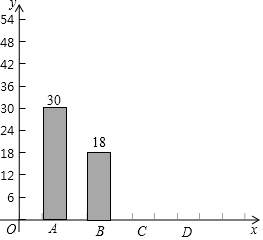 深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.
深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.| 类型 | 频数 | 频率 |
| A | 30 | x |
| B | 18 | 0.15 |
| C | m | 0.40 |
| D | n | y |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
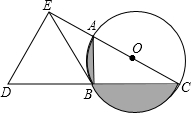 如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.
如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com