某同学的身高为1.4米，某一时刻他在阳光下的影长为1.2米，此时，与他相邻的一棵小树的影长为3.6米，则这棵树的高度为 米．
一本好题口算题卡系列答案科目：初中数学 来源： 题型：单选题
如图，△ABC中，D、E分别是AB、AC上的点，DE∥BC，DE＝1，BC＝3，AB＝6，则AD的长为（ ）
A．1 B．1.5 C．2 D．2.5
查看答案和解析>>
科目：初中数学 来源： 题型：填空题
如图，直线l与半径为4的⊙O相切于点A，P是⊙O上的一个动点（不与点A重合），过点P作PB⊥l，垂足为B，连接PA．设PA＝x，PB＝y，则（x－y）的最大值是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：填空题
如图，在△ABC中∠A=60°，BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，连接PM，PN，则下列结论：①PM=PN；② 
；③△PMN为等边三角形； ④当∠ABC=45°时，BN=
PC．其中正确的是__________.
查看答案和解析>>
科目：初中数学 来源： 题型：填空题
如图，点A1，A2，A3，A4，…，An在射线OA上，点B1，B2，B3，…，Bn―1在射线OB上，且A1B1∥A2B2∥A3B3∥…∥An﹣1Bn﹣1，A2B1∥A3B2∥A4B3∥…∥AnBn﹣1，△A1A2B1，△A2A3B2，…，△An﹣1AnBn﹣1为阴影三角形，若△A2B1B2，△A3B2B3的面积分别为1、4，则△A1A2B1的面积为__________；面积小于2014的阴影三角形共有__________个．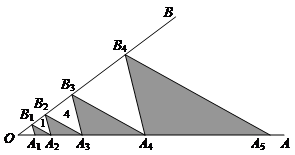
查看答案和解析>>
科目：初中数学 来源： 题型：填空题
如图(1)，将一个正六边形各边延长，构成一个正六角星形AFBDCE，它的面积为1；取△ABC和△DEF各边中点，连接成正六角星形A1F1B1D1C1E1，如图(2)中阴影部分；取△A1B1C1和△D1E1F1各边中点，连接成正六角星形A2F2B2D2C2E2，如图(3)中阴影部分；如此下去…，则正六角星形A4F4B4D4C4E4的面积为________．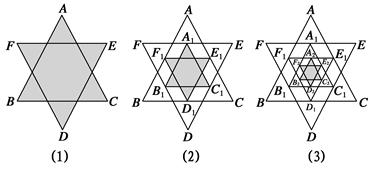
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
∽
，且相似比为
，若
边上的中线
，则
边上的中线
= ．
，则
=__________.